Binomische Formeln und deren Anwendung verstehen

Florian Thüroff·09.05.2023

Die binomischen Formeln gehören zum Grundhandwerkszeug für jeden, der in der Schule oder im Beruf mit der Umformung und Vereinfachung mathematischer Ausdrücke zu tun hat. Die allermeisten Schüler werden in der 7. Klasse mit den drei berühmten binomischen Formeln konfrontiert und werden diese ein (Schul?)-Leben lang auch nicht mehr los 😉.

In diesem Blogartikel erkläre ich dir, was genau die binomischen Formeln sind, wo sie herkommen und wo man die Formeln überall anwenden kann. Im Abschnitt Aufgabentypen und Techniken findest du außerdem eine kurze Übersicht zu den gängigsten Aufgabentypen, die dir in Exen und Schulaufgaben vermutlich immer wieder begegnen 🚀.

Wenn du Übungsaufgaben zu den binomischen Formeln suchst, wirst du in unserem Aufgabengenerator fündig. Dort kannst du dir kostenlos so viele Aufgaben (mit Lösung) erstellen lassen, wie du möchtest 🤓!

Voraussetzungen

Ausmultiplizieren von Klammerausdrücken

Du solltest verstehen, warum

3(4+5)=3·4+3·5

ist.

Hier findest du den Wikipedia-Artikel zum Distributivgesetz.

Rechnen mit Variablen

Du solltest mit Variablen rechnen können, also zum Beispiel verstehen, warum

c(2a + 4b - a) = ac+4bc

ist.

Hier findest du einen Wikipedia-Artikel zu Variablen in der Mathematik.

Was genau sind die binomischen Formeln?

Es gibt insgesamt drei formelmäßige Zusammenhänge, die in der Mathematik unter den Namen erste, zweite und dritte binomische Formel, oder manchmal auch als “Plus-Formel”, “Minus-Formel” und “Plus-Minus-Formel” bekannt sind:

\begin{aligned}&&(a+b)^2=a^2+2ab+b^2\quad\text{(1. binomische Formel)}\\&&(a-b)^2=a^2-2ab+b^2\quad\text{(2. binomische Formel)}\\&&(a+b)(a-b)=a^2-b^2\quad\text{(3. binomische Formel)}\end{aligned}

Anders als viele andere Zusammenhänge in der Mathematik sind die Formeln übrigens nicht nach ihrem Erfinder benannt (nein, die Formeln sind NICHT nach einem italienischen Mathematiker namens Alessandro oder Francesco Binomi benannt). Für den unwahrscheinlichen Fall, dass es dir irgendwann einmal in der Beantwortung der Millionenfrage hilft: Die Formeln gehen zurück auf das Wort “Binom”, mit dem in der Mathematik schlicht zweigliedrige Ausdrücke (wie z.B. $a+b$ oder $a-b$ ) bezeichnet werden. Die binomischen Formeln sind also einfach Formeln für die Quadrate von Binomen 😜.

Woher kommen die binomischen Formeln? Durch die algebraische Brille.

Eine Möglichkeit die binomischen Formeln herzuleiten besteht darin, sich Erinnerung zu rufen, nach welchen Regeln in der Algebra Klammern ausmultipliziert werden und dann einfach von links nach rechts zu rechnen.

Zur Herleitung der ersten binomischen Formel rechnet man wie folgt:

\begin{aligned}(a+b)^2&=&(a+b)\cdot(a+b)\\&=&a\cdot(a+b)+b\cdot(a+b)\\&=&a^2+ab+ba+b^2\\&=&a^2+2ab+b^2.\end{aligned}

In der ersten Zeile haben wir dabei einfach nur das Quadrat aufgelöst und als Multiplikation des Klammerausdrucks $(a+b)$ mit sich selbst geschrieben. In der zweiten und dritten Zeile haben wir dann die Klammern ausmultipliziert. Dazu haben wir in Zeile 2 zuerst die linke Klammer aufgelöst und die rechte Klammer wie eine einfache Zahl behandelt. Daraus ergeben sich zwei Summenterme, die wir in der dritten Zeile weiter ausmultipliziert haben. In der vierten Zeile schließlich haben wir nur noch zwei Terme zusammengefasst ( $ab + ba = ab + ab = 2ab$ ) um die rechte Seite der ersten binomischen Formel zu erhalten 🥳 !

Die Herleitung der zweiten binomischen Formel funktioniert genauso:

\begin{aligned}(a-b)^2&=&(a-b)\cdot(a-b)\\&=&a\cdot(a-b)-b\cdot(a-b)\\&=&a^2-ab-ba+b^2\\&=&a^2-2ab+b^2,\end{aligned}

wobei du dich hier immer an die Regeln “Minus mal Minus ergibt Plus” und “Plus mal Minus ergibt Minus” erinnern musst.

Die Herleitung der dritten binomische Formel geht sogar noch einfacher:

\begin{aligned}(a+b)\cdot(a-b)&=&a\cdot(a-b)+b\cdot(a-b)\\&=&a^2-ab+ba-b^2\\&=&a^2-b^2,\end{aligned}

wobei wir $ab-ba=ab-ab=0$ verwendet haben. Fertig 🤩.

Woher kommen die binomischen Formeln? Durch die geometrische Brille.

Neben der streng formalen Herleitung der binomischen Formeln, so wie im vorherigen Abschnitt gezeigt, gibt es auch noch eine zweite, visuell anschauliche Methode, sich die binomischen Formeln klarzumachen. Der Trick dabei ist immer, sich die Ausdrücke $a^2$ und $b^2$ als die Flächen von Quadraten mit Seitenlängen $a$ und $b$ vorzustellen und Produkte der Form $a\cdot b$ als die Fläche eines Rechtecks mit Seitenlängen $a$ und $b$ zu interpretieren. Davon ausgehend kann man die drei binomischen Formeln als geometrische Beziehungen zwischen Quadraten und Rechtecken unterschiedlicher Größe verstehen. Wie das genau im Einzelfall funktioniert, zeige ich dir in den folgenden Abschnitten.

Die Geometrie hinter der ersten binomischen Formel

Geometrische Veranschaulichung der ersten binomischen Formel

Wir starten mit einer geometrischen Erklärung der ersten binomischen Formel und gehen aus von einem Quadrat mit einer Seitenlänge $7$ und einer Fläche $7^2=49$ , wie in der Abbildung gezeigt.

Ob du’s glaubst oder nicht: Die erste binomische Formel ist im Grunde nix weiter als ein Kochrezept, wie man die große Quadratfläche (Seitenlänge 7) in kleinere Quadrat- und Rechteckflächen aufteilen kann. Angenommen wir teilen das große Quadrat in zwei kleine Quadrate mit Seitenlängen 4 und 3 auf (7 = 4 + 3). Die Aufteilung ist im rechten (bzw., falls du die mobile Version betrachtest, unteren) Teil der oberen Abbildung angedeutet. Wie du siehst, ist die große Quadratfläche (im Bild rot dargestellt) größer als die Summe der beiden kleineren Quadratflächen (im Bild blau und lila schattiert), d.h. $7^2=(4+3)^2>4^2+3^2$ . Der Grund: Wenn man die beiden kleineren Quadrate, wie im Bild angedeutet, Ecke an Ecke in das größere Quadrat einpasst entstehen zwei rechteckige “Löcher” (im Bild grau dargestellt), die man zu den beiden kleineren Quadratflächen dazuzählen muss um auf die ursprüngliche (größere) Quadratfläche zu kommen.

OK, und wie groß sind diese zwei Rechtecke? Wie du siehst grenzen die Rechtecke mit jeweils einer Seite an das 4-er Quadrat und mit einer Seite an das 3-er Quadrat an. Die Fläche der Rechtecke ist also $4\cdot3$ .

Zusammengefasst setzt sich die ursprüngliche Quadratfläche $7^2=(4+3)^2$ neben den beiden kleineren Quadratflächen $4^2$ und $3^2$ aus ZWEI rechteckigen Flächen der Größe $4\cdot3$ zusammen, so dass insgesamt gilt:

7^2=(4+3)^2=4^2+2\cdot(4\cdot3)+3^2.

Kommt dir das irgendwie bekannt vor? Genau, das ist die erste binomische Formel! An der Aufteilung des großen 7-er Quadrats in kleinere 4-er und 3-er Quadrate war übrigens nichts speziell. Wir hätten das Quadrat genauso gut in ein 5-er und ein 2-er Quadrat zerlegen können (wie beispielsweise in der linken bzw. am Smartphone in der oberen Hälfte der Abbildung gezeigt). Die Erklärung ist die gleiche. Noch allgemeiner: Wenn du in der gefundenen Beziehung $(4+3)^2=4^2+2\cdot(4\cdot3)+3^2.$ die Zahlen $4$ und $3$ durch die Platzhalter $a$ und $b$ ersetzt, findest du die erste binomische Formel in genau der Form, in der wir sie in Kapitel Was genau sind die binomischen Formeln? geschrieben haben 🤓 !

Die Geometrie hinter der zweiten binomischen Formel

Auch für die zweite binomische Formel gibt es eine anschauliche Erklärung über Quadratflächen. Aber anstatt eine große Quadratfläche aus kleineren Flächen zusammenzusetzen, versuche wir jetzt eine kleinere Quadratfläche aus einer großen Fläche “herauszuschälen” 😄 . Die generelle Idee ist wieder in der folgenden Abbildung gezeigt:

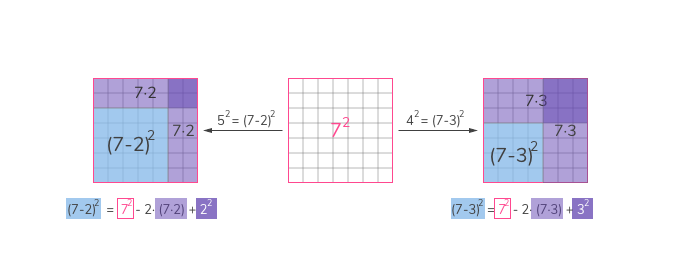
Geometrische Veranschaulichung der zweiten binomischen Formel

Wir starten wieder mit einem großen Quadrat der Seitenlänge 7 und versuchen ein kleineres Quadrat der Seitenlänge $4=7-3$ herausschälen. Wie im rechten (bzw., falls du die mobile Version betrachtest, unteren) Teil der Abbildung dargestellt, müssen wir dazu zwei rechteckige Streifen der Breite 3 (und Länge 7) wegpopeln. Jeder dieser Streifen besitzt eine Fläche von $7\cdot3=21$ , so dass wir (unvorsichtigerweise) folgern könnten: $4^2=(7-3)^2=7^2-2\cdot(7\cdot3)$ (falsch!).

Allerdings kann man ganz leicht nachprüfen dass das falsch ist:

4^2=(7-3)^2=16\neq7^2-2\cdot(7\cdot3)=7

Aber was genau läuft schief 🤔 ? Ganz einfach! Wir haben zu viel weggepopelt! Wie du in der Abbildung siehst, überlappen sich die beiden rechteckigen Streifen und die Fläche des Überlapps (ein Quadrat der Seitenlänge 3, also der Fläche 9) macht genau den Fehlbetrag in obiger Rechnung aus 🤗 ! Wir haben das Quadrat (den Überlapp) einmal zu viel abgezogen, also müssen wir’s wieder einmal dazuzählen. Wir erhalten also insgesamt:

(7-3)^2=7^2-2\cdot(7\cdot3)+3^2,

also genau die zweite binomische Formel 🤓 ! Wiederum: Der Trick mit dem Überlapp klappt immer und hat nichts mit der speziellen Wahl unseres Beispiels zu tun. In der linken (am Smartphone in der unteren) Hälfte der Abbildung siehst du, dass der gleiche Effekt auftritt, wenn man beispielsweise versucht, ein Quadrat der Seitenlänge 5 aus dem großen Quadrat herausschälen. Der Trick funktioniert ganz allgemein und die zweite binomische Formel in der in Kapitel Was genau sind die binomischen Formeln? dargestellten Form ergibt sich wieder, indem du die Zahlen $7$ und $3$ in unserem Beispiel durch die Platzhalter $a$ und $b$ ersetzt.

Die Geometrie hinter der dritten binomischen Formel

Zu guter Letzt schauen wir uns noch die geometrische Deutung der dritten binomischen Formel an, die so etwas wie eine Beziehung zwischen der Fläche $(a+b)(a-b)$ eines Rechtecks mit Seitenlängen $a+b$ und $a-b$ einerseits und der Differenz aus zwei Quadratflächen $a^2$ und $b^2$ andererseits herstellt.
Um die Dinge anschaulicher zu machen, haben wir die Idee in der folgenden Abbildung wieder in Form eines konkreten Beispiels dargestellt:

Geometrische Veranschaulichung der dritten binomischen Formel

Im Falle der dritten binomischen Formel

(a+b)(a-b)=a^2-b^2

ist es am einfachsten, von der rechten Seite der Gleichung auszugehen und sich die linke Seite “zu bauen”. Wenn wir uns also, wie immer, $a^2$ und $b^2$ als die Flächen zweier Quadrate vorstellen, dann ist die rechte Seite der dritten binomischen Formel die Anweisung, das b-Quadrat vom a-Quadrat wegzunehmen. In der Abbildung (links bzw., falls du mobil unterwegs bist, oben) haben wir das für den Fall $a=7$ und $b=2$ dargestellt.

Die Fläche $7^2-2^2$ bekommen wir, indem wir das kleine lila 2-er Quadrat aus dem größeren roten 7-er Quadrat herausschneiden. Wenn wir das machen (Abbildung Mitte bzw. unten links für die mobile Version) bekommen wir allerdings erstmal ein “angefressenes” Quadrat und nicht direkt ein Rechteck. Allerdings können wir (ohne die Fläche des angefressenen Quadrats zu verändern) einfach Friseur spielen und den im Bild blau gefärbten rechteckigen Überstand (mit Seitenlängen $2$ und $7-2$ ) entlang der angedeuteten Linie abschneiden. Praktischerweise ist die lange Seite des abgeschnittenen blauen Rechtecks ( $7-2$ ) genauso lang wie die kurze Seite des übrigbleibenden weißen Rechtecks (ebenfalls $7-2$ ).

Wenn wir also im letzten Schritt die beiden Rechtecke an der gleich langen Seite wieder zusammenkleben (im Bild rechts) entsteht ein neues, größeres Rechteck mit den Seitenlängen $7+2$ und $7-2$ und der Fläche $(7+2)\cdot(7-2)$ . Fällt dir etwas auf? Richtig! Das ist die dritte binomische Formel:

7^2-2^2=(7+2)(7-2)

🥳 Wie immer lässt sich unser Beispiel auf beliebige andere Zahlen anwenden. Wenn wir wieder die Zahlen $7$ und $2$ durch die Buchstaben $a$ und $b$ ersetzen, erhalten wir die dritte binomische Formel in der in Kapitel Was genau sind die binomischen Formeln? angegebenen Form 🤓 .

Aufgabentypen und Techniken

Gut, du weißt jetzt hoffentlich schon etwas mehr über die binomischen Formeln. Aber wozu das Ganze? In den folgenden Abschnitten gebe ich dir einen Überblick über mögliche Anwendungsfälle und Aufgabentypen, die dir im Laufe deines Schullebens und auch im späteren Leben noch begegnen könnten.

Wenn einiges von dem, was ich dir in den nächsten kurzen Abschnitten vorstelle neu und unverständlich für dich klingt, mach dir keine Sorgen 🙃 ! Ich möchte dir nur zeigen, wozu binomische Formeln noch nützlich sein werden. Du musst nicht alle Anwendungen direkt verstehen.

Binomische Formeln vorwärts anwenden

Der einfachste Aufgabentyp, dem du in der Schule vor allem kurz nach Einführung der binomischen Formeln begegnen wirst, zielt einfach auf eine direkte Anwendung der (auswendig gelernten) Formeln ab.

Im einfachsten Fall wirst du Aufgaben mit einer Variablen (Platzhalter) begegnen, wie zum Beispiel (Lösung in rot):

(a-5)^2=\color{red}{a^2-10a+25}.

Etwas schwieriger sind dann Aufgaben, in denen die Variable von einer Zahl (einem Koeffizienten) multipliziert wird, zum Beispiel:

(3a+4)^2=\color{red}{9a^2+24a+16}.

In der nächsten Schwierigkeitsstufe bekommst du es mit zwei Variablen zu tun, zum Beispiel:

(2a-5b)^2=\color{red}{4a^2-20ab+25b^2}.

Und schließlich wirst du teilweise noch Aufgaben von der Bauart des letzten Beispiels sehen, die zusätzlich noch einen Vorfaktor vor der Klammer haben, zum Beispiel

5(3a+6b)^2=\color{red}{45a^2-180ab+180b^2}.

Binomische Formeln rückwärts anwenden und Terme vereinfachen

Die zweite Form von Aufgaben, denen du in der Schule kurz nach Einführung der binomischen Formeln begegnen wirst, zielen auf die Anwendung der binomischen Formeln “rückwärts” ab, mit dem Ziel, Terme zu vereinfachen.

Zum Beispiel (Lösung wieder in rot)

a^2+6a+9=\color{red}{(a+3)^2}.

Im schwierigsten Fall wirst du zur Vereinfachung von Termen gemeinsame Faktoren erkennen müssen, die du ausklammern musst bevor du eine binomische Formel anwenden kannst, wie im folgenden Beispiel gezeigt:

\begin{aligned}12a^2+36a+27&=&\color{red}{3(4a^2+12a+9)}\\&=&\color{red}{3(2a+3)^2}.\end{aligned}

Quadratische Ergänzung

Eine extrem wichtige Anwendung der binomischen Formeln ist die sogenannte quadratische Ergänzung, der du in der Schule wahrscheinlich spätestens im Zusammenhang mit der Diskussion von quadratischen Funktionen (Parabeln) begegnen wirst. Dabei geht es darum, einen allgemeinen quadratischen Ausdruck als Summe aus einer binomischen Formel und einem konstanten Term darzustellen.

Zum Beispiel kann man aus der Umformung

\begin{aligned}4x^2-16x+20&=&(4x^2-16x+16)+4\\&=&(2x-4)^2+4\end{aligned}

direkt den Scheitelpunkt einer Parabel ablesen. Außerdem kann man mit dem Trick der quadratischen Ergänzung eine allgemeine (als “Mitternachtsformel” bekannte) Lösung zur Nullstellensuche quadratischer Gleichungen herleiten. Und selbst Profis verwenden die quadratische Ergänzung und damit die binomischen Formeln an vielen Stellen, beispielsweise der Berechnung spezieller (sogenannter Gauß’scher) Integrale, die in der Mathematik, Naturwissenschaften und Technik eine extrem wichtige und prominente Rolle spielen.

Gebrochen rationale Funktionen

Eine weitere Anwendung, die dir in der Schule (und, solltest du einen mathematisch geprägten Beruf ergreifen auch später) noch behilflich sein wird, ist die Vereinfachung und Manipulation sogenannter gebrochen rationaler Funktionen.

Wenn du beispielsweise das Verhalten der Funktion

f(x)=\frac{x^2-2x+1}{x-1}

für $x\rightarrow1$ untersuchen sollst, ist es hilfreich die binomischen Formeln zu kennen, mit deren Hilfe wir den Grenzwert leicht ermitteln können:

\begin{aligned}\lim_{x\rightarrow1}\frac{x^2-2x+1}{x-1}&=&\lim_{x\rightarrow1}\frac{(x-1)^2}{x-1}\\&=&\lim_{x\rightarrow1}(x-1)=0.\end{aligned}

Rechentricks

Eine witzige und nützliche Anwendung der binomischen Formeln stellen Kopfrechentricks dar. Zum Beispiel kann man die ersten beiden binomischen Formeln wunderbar verwenden, um “schwierige” Quadratzahlen im Kopf zu berechnen, die nahe an einer glatten Zahl liegen. Zum Beispiel kann man

59^2=3481

mit der binomischen Minus-Formel ganz leicht im Kopf ausrechnen, wenn man

59^2=(60-1)^2=60^2-2\cdot60+1=3481

verwendet.

Die dritte binomische Formel lässt sich wunderbar verwenden, um große Zahlen zu multiplizieren, die von einer glatten Zahl nach oben und unten gleich weit entfernt sind. Zum Beispiel lässt sich

42\cdot38=1596

blitzschnell im Kopf rechnen, wenn man anstatt stur zu rechnen die dritte binomische Formel benutzt:

\begin{aligned}42\cdot38&=&(40+2)(40-2)\\&=&40^2-2^2=1600-4=1596.\end{aligned}

Eine weitere Anwendung der ersten binomischen Formel zur blitzschnellen Quadrierung von zweistelligen Zahlen die auf 5 enden zeige ich dir in diesem Blogartikel.

Fragen und Antworten

Gibt es mehr als drei binomische Formeln?

Unter dem Namen binomische Formeln versteht man in aller Regel genau die drei Formeln, die wir in diesem Artikel besprochen haben. Es gibt allerdings mit dem sogenannten binomischen Lehrsatz sehr wohl eine Erweiterung der Formeln auf beliebige Potenzen. Der Satz besagt ganz allgemein

(a+b)^n=\sum_{k=0}^n\binom{n}{k}x^kn^{n-k}

und die ersten beiden binomischen Formeln sind schlicht Spezialfälle dieser allgemeineren Formel für

n=2

Gelten die binomischen Formeln auch für komplexe Zahlen?

Ja, das tun sie! Dort sind die binomischen Formeln sogar besonders häufig anzutreffen, weil jede komplexe Zahl

z

als Binom (also zweigliedriger Ausdruck der Form

z=a+ib

) dargestellt werden kann. Die binomischen Formeln sind daher wichtig zur Berechnung von Quadraten komplexer Zahlen. Zum Beispiel ist

z^2=(a+ib)^2=a^2-b^2+2ib

(wobei das Vorzeichen des

b^2

-Terms negativ sein muss, weil

i^2=-1

Dürfen auch mehr als 3 Terme in der Klammer stehen?

Natürlich kann man so viele Terme in die Klammer schreiben, wie man möchte und immer noch damit rechnen. Streng genommen würde man dann aber nicht mehr von Binomen (also ZWEIgliedrigen) Ausdrücken sprechen und eine Formel wie

(a+b+c)^2=a^2+b^2+2(ab+bc+ac)

auch nicht mehr als binomische Formel bezeichnen. Solche Zusammenhänge für mehrgliedrige Ausdrücke werden in der Mathematik allgemein unter dem “Multinomialtheorem” abgehandelt.

Mehr zu natürlichen Zahlen

Du suchst detailierte Informationen, wie zum Beispiel alle Teiler oder die Vielfachenmenge, zu einer bestimmten natürlichen Zahl? Dann wirst du hier fündig.

1-20

21-40

41-60

61-80

81-100

101-120

121-140

141-160

161-180

181-200

Binomische Formeln und deren Anwendung verstehen