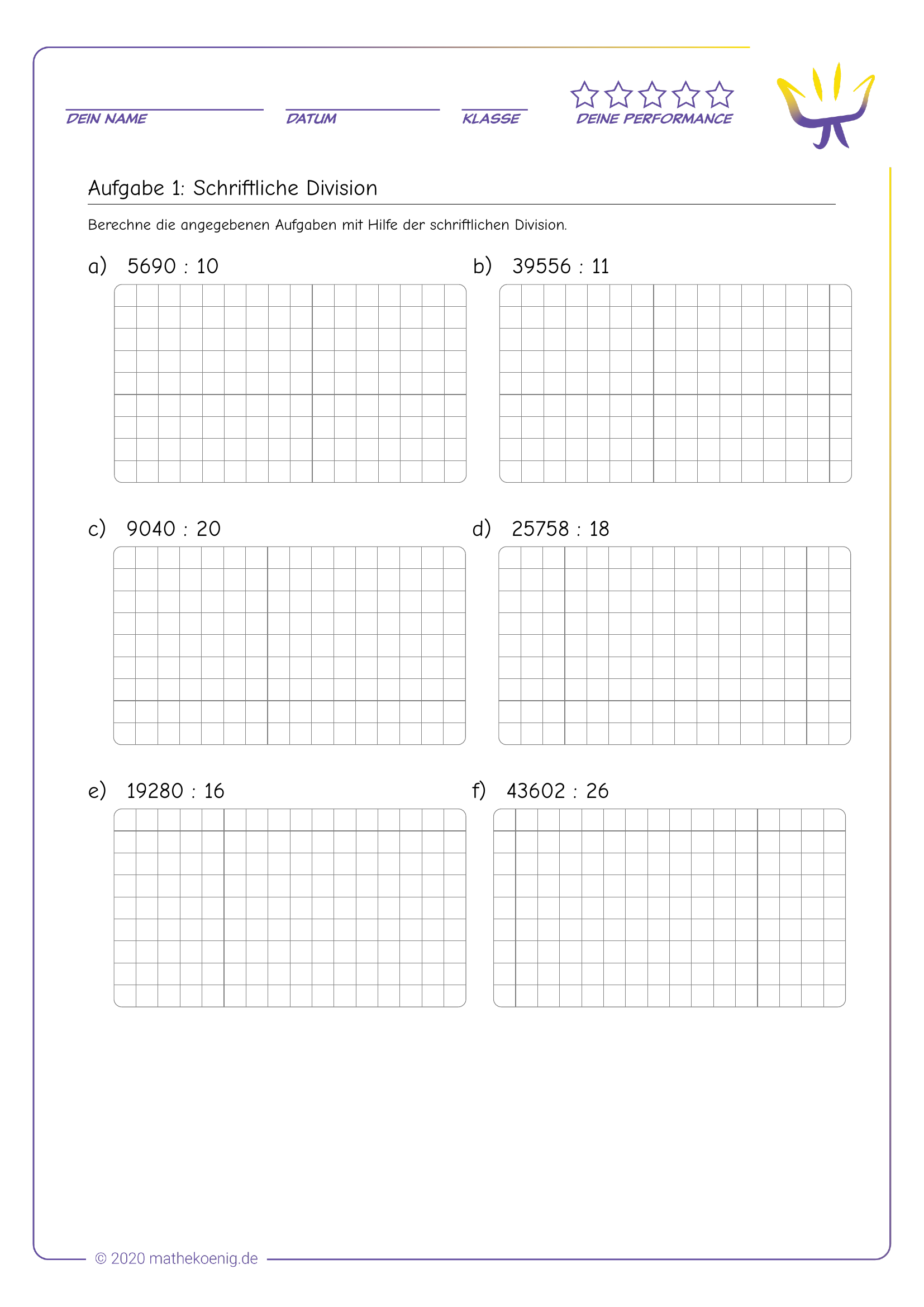
Schriftlich Multiplizieren einfach erklärt
Verstehe wie die schriftliche Multiplikation funktioniert und stelle dir individuelle Übungsblätter samt Lösungen zum Thema zusammen.
30.11.2023·Grundrechenarten erklärt
MathekönigSchriftliches Dividieren einfach erklärt
Florian Thüroff·09.05.2023
Wenn du diesen Artikel liest, kennst du dich wahrscheinlich schon ein bisschen mit den vier Grundrechenarten aus und weißt, wie man zwei Zahlen durcheinander teilen kann. Zumindest, so lange die beiden Zahlen klein genug sind und du das kleine Einmaleins beherrscht.
Dummerweise reicht das kleine Einmaleins allein nicht aus um große Zahlen zu dividieren 😩. Zur Division von Zahlen größer als 100 verwendet man am besten ein Rechenverfahren, das “schriftliche Division” genannt wird und das ich in den nachfolgenden Abschnitten genauer erkläre.
Voraussetzungen
Wie immer, bevor es losgeht, gebe ich dir hier einen kurzen Überblick über die Themen und Fähigkeiten, die du mitbringen solltest um die schriftliche Division zu verstehen.
Kopfrechnen (kleines Einmaleins)
Grundschule (1. & 2. Klasse)
Schriftliches Subtrahieren
Grundschule (3. & 4. Klasse)
Außerdem verwende ich im Artikel häufig die Begriffe “Dividend” und “Divisor”. Solltest du nicht wissen, was damit gemeint ist, schau vorher kurz im Abschnitt Fragen und Antworten nach. Dort werden die Begriffe erklärt.
Das Kochrezept: So funktioniert die schriftliche Division 🚀
Um dir das Kochrezept zum schriftlichen Dividieren zu zeigen, lass uns einfach Schritt für Schritt durch die Lösung der folgenden Divisionsaufgabe gehen:
Solltest du die Aufgabe im Kopf rechnen können, ziehe ich meinen Hut. Meine Kopfrechenkünste übersteigt die Aufgabe bei weitem! Aber wozu gibt es schließlich schriftliche Rechenverfahren 😎.
Schritt 1: Den Dividenden zerlegen 👈
Im ersten Schritt nehmen wir uns den Dividenden (die Zahl links neben dem Divisionszeichen) zur Burst und suchen uns ausgehend von der ganz linken Ziffer (in unserem Beispiel die 2) die kleinste Zahl aus, die größer oder gleich dem Divisor (also der Zahl 13) ist.
In unserem Rechenbeispiel starten wir also direkt mit der ganz linken Ziffer und bilden zunächst einmal die Zahl 2. Da 2 kleiner ist als unser Divisor (die Zahl 13), nehmen wir auch noch die nächste Ziffer mit, um aus den ersten beiden Ziffern des Dividenden die Zahl 22 zu bilden.
Schritt 2: Die kleine Divisionsaufgabe lösen 👈
Im zweiten Schritt lösen wir eine “kleine Divisionsaufgabe”, indem wir die im ersten Schritt gebildete Zahl 22 durch 13 teilen. Natürlich lässt sich streng genommen die Zahl 22 gar nicht (ohne Rest) durch 13 teilen. Aber das ist OK. Wir überlegen uns einfach, wie oft die 13 vollständig in die 22 passt und notieren uns diese Zahl als erste Ziffer des gesuchten Ergebnis auf der rechten Seite der Gleichung.
Da die 13 genau einmal in die 22 passt, notieren wir uns also die 1 als erste Ergebnisziffer nach dem Gleichheitszeichen.
Schritt 3: Die kleine Multiplikationsaufgabe lösen 👈
Im dritten Schritt multiplizieren wir die Ergebnisziffer, die wir uns in Schritt 2 notiert haben mit unserem Divisor (also der Zahl 13) und schreiben das Ergebnis unter die beiden Ziffern des Dividenden, die wir im ersten Schritt bestimmt haben.
In unserem Falle rechnen wir also
Schritt 4: Den Rest bestimmen 👈
Im vierten Schritt berechnen wir uns den Rest der kleinen Divisionsaufgabe aus dem zweiten Schritt.
Dazu ziehen wir die eben berechnete Zahl 13 von der Zahl 22 ab und notieren uns das Ergebnis 9. Um die Minusaufgabe zu berechnen (du erinnerst dich: Ich bin schlecht im Kopfrechnen 😜 ), verwende ich die schriftliche Subtraktion.
Schritt 5: Die nächste kleine Divisionsaufgabe bestimmen 👈
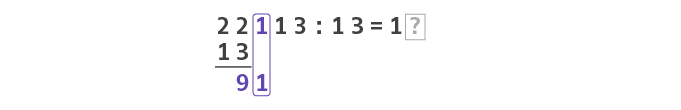
Um weiterrechnen zu können, suchen wir uns jetzt die nächste Ziffer des Dividenden, die wir bisher noch nicht “verarbeitet” haben und bilden aus dieser Ziffer und dem im vorherigen Schritt berechneten Rest eine neue Zahl, mit der wir weiter rechnen können.
Da wir im Laufe der ersten vier Schritte bereits die ersten beiden Ziffern (2 und 2) des Dividenden 22113 “verarbeitet” haben, kommt als nächstes die Ziffer 1 an die Reihe, die wir rechts neben den eben berechneten Rest 9 schreiben, um mit der Zahl 91 weiterzumachen.
Schritt 6: Schritte 2 bis 5 wiederholen 👈
Sobald wir Schritt 5 erledigt haben, geht es wieder zurück zu Schritt 2 (außer dass wir jetzt mit der Zahl 91 anstelle der Zahl 22 rechnen). Um das Endergebnis zu berechnen müssen wir einfach Schritte 2 bis 5 so oft wiederholen, bis wir alle Ziffern des Dividenden “verarbeitet” haben, wir also in Schritt 5 keine Ziffern im Dividenden mehr übrig haben, aus denen wir die nächste kleine Divisionsaufgabe bestimmen könnten. An diesem Punkt haben wir alle Ergebnisziffern berechnet und die Divisionsaufgabe gelöst!
OK, ich weiß, dass ich euch die vollständige Lösung der Aufgabe noch schuldig bin, deshalb lasst uns einfach gemeinsam die Anweisung aus Schritt 6 für unsere Beispielaufgabe durchführen:
Zunächst einmal müssen wir die nächste kleine Divisionsaufgabe (Schritt 2) lösen, indem wir 91 (die Zahl die wir im fünften Schritt erzeugt haben) durch 13 teilen. Da die 13 sieben mal in die 91 passt, notiere ich mir die 7 als nächste Ergebnisziffer auf der rechten Seite der Gleichung.
Weiter zu Schritt 3, in dem wir die eben berechnete Ergebnisziffer 7 mit der 13 multiplizieren, und das Ergebnis unter den Dividenden der kleinen Divisionsaufgabe, also unter die 91 schreiben. Wie wir sehen (Schritt 4) geht dieses Mal alles genau auf und es bleibt kein Rest übrig 😳 ?! Heißt das wir sind jetzt fertig? Nein! Schließlich sind ja noch nicht alle Ziffern im Dividenden verarbeitet (von der Zahl 22113 müssen die beiden letzten Ziffern 1 und 3 noch verarbeitet werden). Also einfach weiter als wäre nix gewesen 😏 !
Die nächste Ziffer die an die Reihe kommt (Schritt 5) ist die 1, die wir wieder neben unseren (nicht vorhandenen) Rest schreiben um mit der Zahl 1 weiterzurechnen.
Also, wieder zurück zu Schritt 2 und überlegen wie oft die 13 in die 1 passt. Genau: Null mal. Aber auch die Null ist eine gültige Ergebnisziffer 😉 . Die nächsten Schritte sind jetzt so einfach, dass ich sie direkt alle zusammengefasst habe: Die Multiplikation Ergebnisziffer mal 13 ergibt 0 (Schritt 3). Und der Rest der bleibt ist 1 (Schritt 4).
Fast fertig! Wir müssen uns nur noch um die letzte unverarbeitete Ziffer im Dividenden, die 3, kümmern. Wir verheiraten den eben berechneten Rest 1 mit der letzten unverarbeiteten Ziffer 3, um mit der Zahl 13 weiterzumachen (Schritt 5).
Nachdem wir mittlerweile gut in Übung sein dürften, fasse ich mich diesmal kurz: Die 13 geht genau ein Mal in die 13, d.h. ich notiere mir die 1 als nächste (und letzte) Ergebnisziffer (Schritt 2). Außerdem ist
Da wir an dieser Stelle alle Ziffern des Dividenden verarbeitet haben sind wir fertig (Schritt 5). Die Divisionsaufgabe ist also vollständig und ohne Rest gelöst:
Wenn’s mal nicht aufgeht: Die Division mit Rest
In gewisser Weise war unsere Beispielaufgabe aus dem letzten Kapitel etwas glücklich gewählt. Am Ende der Aufgabe ging alles genau auf. Die letzte Subtraktion hinterlässt keinen Rest. Bei vielen Divisionsaufgaben werden wir allerdings nicht so viel Glück haben und die Division geht nicht mehr genau auf, d.h. die letzte Subtraktion ergibt nicht mehr Null. In diesen Fällen spricht man von einer Division mit Rest.
Die gute Nachricht: Die schriftliche Division mit Rest funktioniert im Grunde genauso wie die schriftlich Division ohne Rest. Der einzige Unterschied: Der in der letzten Subtraktion berechnete Rest wird im Ergebnis mit angegeben. Wie genau zeige ich dir am besten wieder an einem Beispiel:
Wie du siehst, befolgt man bei der Division mit Rest das Standard-Kochrezept der schriftlichen Division, indem man Schritt für Schritt alle Ziffern des Dividenden verarbeitet, bis keine unverarbeiteten Ziffern mehr übrig sind.
Im obigen Beispiel habe ich das für die Aufgabe
Für Profis: Division mit Komma
Für die echten Mathe-Enthusiasten unter euch sei erwähnt, dass die oben beschriebene Division mit Rest im Rahmen der natürlichen (und ganzen) Zahlen die “richtige” Berechnungsvorschrift zur Bildung von Quotienten (so nennt man das Ergebnis der Division zweier Zahlen) ist, da weder die Menge der natürlichen noch die der ganzen Zahlen “Kommazahlen” beinhalten.
Lässt man allerdings zu, dass das Ergebnis der Rechnung in einer größeren Zahlenmenge liegen darf (bspw. der Menge der sogenannten rationalen Zahlen), dann lässt sich das in diesem Blog-Artikel beschriebene schriftliche Divisionsverfahren erweitern auf die schriftliche Division mit Komma, die wir euch in einem separaten Blog-Beitrag erklären.
Häufige Fehler
Unsauberes Arbeiten
Bei der schriftlichen ist es wichtig, dass du alle Zahlen und Ziffern in deiner Rechnung sauber untereinander schreibst. Arbeitest du unsauber läufst du Gefahr, dass du den Überblick verlierst, welche Ziffern voneinander subtrahiert werden müssen, bzw. welche Ziffern des Dividenden noch verarbeitet werden müssen. Vergisst du Dividenden-Ziffern zu verarbeiten, oder subtrahierst du die falschen Ziffern, berechnest du unweigerlich ein falsches Ergebnis!
Vergessen der Null als Ergebnisziffer
Lass dich nicht verunsichern, wenn du im Laufe der Rechnung “kleine Divisionsaufgaben” lösen musst, in denen der Dividend kleiner als der Divisor ist. Du erinnerst dich: Wir sind der Situation in unserem Rechenbeispiel
Rechenfehler bei der Multiplikation und Subtraktion
Achte darauf, bei den kleinen Hilfsrechnungen keine Fehler zu machen. In der schriftlichen Division hängt jeder Rechenschritt von den vorhergehenden Rechenschritten ab, so dass in aller Regel auch “richtig” berechnete Ergebnisziffern falsch sind, wenn dir vorher in der Rechnung ein Fehler unterlaufen ist.
Schriftliche Division - Aufgaben mit Lösungen
Falls du gerne die schriftliche Division üben möchtest, dann hast du hier die Gelegenheit dir entweder bereits fertige Übungsblätter herunterzuladen, in unserem Aufgabengenerator eigene Übungsblätter zusammenzustellen oder direkt mit unserem Trainingscenter zu starten 🚀.
Fragen und Antworten
Der Dividend ist diejenige Zahl, die in einer Divisionsaufgabe geteilt wird. Zum Beispiel wird in der Aufgabe
Der Divisor ist diejenige Zahl, durch die in einer Divisionsaufgabe geteilt wird. Zum Beispiel wird in der Aufgabe
Der Quotient ist ist das Ergebnis einer Divisionsaufgabe. Zum Beispiel wird in der Aufgabe
Nein. Zwar arbeitet man in der höheren Mathematik häufig mit sogenannten Grenzwertberechnungen, in denen sich der Divisor der Zahl Null annähert. Aber das Teilen durch die Zahl Null selbst ist in dem Sinne “verboten”, als dass das “Ergebnis” einer solchen Aufgabe keine mathematisch sinnvolle Interpretation hat.
Ja, das geht. In dem Fall kann man entweder ein Ergebnis mit Rest angeben (zum Beispiel
Das könnte dich auch interessieren
