Größter gemeinsamer Teiler (ggT) - leicht erklärt

Stefan Vickers·09.05.2023

Titelbild zum Blog Artikel größter gemeinsamer Teiler zweier natürlicher Zahlen

Den größten gemeinsamen Teiler zweier natürlicher Zahlen zu kennen, ist insbesondere dann von Nutzen, wenn es darum geht, Brüche effizient zu kürzen. Wir zeigen dir in diesem Blogartikel drei verschiedene Möglichkeiten, wie man den größten gemeinsamen Teiler, auch ggT genannt, finden kann und erklären welche Stärken und Schwächen die unterschiedlichen Rechenvorschriften mit sich bringen.

Bist du nicht auf der Suche nach Erklärungen, sondern nach Aufgaben zum Üben? Dann springe gleich zu unserem Aufgabengenerator und drucke dir kostenlos so viele Übungsblätter als PDF 📃 aus wie du rechnen kannst.

Größter gemeinsamer Teiler - Worum geht’s?

Der Begriff “größter gemeinsamer Teiler” zweier natürlicher Zahlen $a,b$ beschreibt bereits recht gut über welche Eigenschaften $ ggT(a,b)$ definiert ist. Um $ggT(a,b)$ zu bestimmen benötigen wir zum einen die Teilermengen der beiden involvierten natürlichen Zahlen $T_a$ und $T_b$ um daraus die gemeinsame Teilermenge $T_{a\cap b} = T_a \cap T_b$ zu bestimmen. Die Menge $T_{a\cap b}$ sollten nun alle Zahlen enthalten, die sowohl Teiler von $a$ als auch Teiler von $b$ sind.

Nehmen wir nun noch das Maximum der gemeinsame Teilermenge, so erhalten wir den größten gemeinsamen Teiler von $a$ und $b$

ggT\left(a,b\right) = max \left(T_a \cap T_b \right)

Um das ganze nicht zu theoretisch zu machen, schauen wir uns folgendes Beispiel an. Wir suchen den größten gemeinsamen Teiler von $a=108$ und $b=84$ . Folgende Zahlen sind Teiler von $108$ bzw. von $84$ :

\begin{aligned}T_{108} &=& \{{\color{green}1};{\color{green}2};{\color{green}3};{\color{green}4};{\color{green}6};9;{\color{green}12};18;27;36;54;108 \} \\ T_{84} &=& \{{\color{green}1};{\color{green}2};{\color{green}3};{\color{green}4};{\color{green}6};7;{\color{green}12};14;21;28;42;84 \}. \end{aligned}

Wir sehen bereits, dass die Teiler $1;2;3;4;6;12$ sowohl Teiler von $108$ als auch $84$ sind. Da wir an den größten gemeinsamen Teiler interessiert sind, folgt

ggT \left( 108, 84 \right) = \max \left\{ 1;2;3;4;6; {\color{green}12} \right\} = 12

Oftmals wird im Zusammenhang mit dem größten gemeinsamen Teiler auch das kleinste gemeinsame Vielfache (kgV) diskutiert. Ähnlich wie beim ggT wird der kgV beim Rechnen mit Brüchen verwendet. Während der ggT eine hilfreiche Rechenvorschrift beim Kürzen von Brüchen darstellt, erleichtert der kgV das Erweitern und damit das Addieren und Subtrahieren von Brüchen.

Voraussetzungen

Folgendes Vorwissen solltest du bereits mitbringen, um den größten gemeinsamen Teiler zweier natürlicher Zahlen bestimmen zu können. Solltest du mit einem der Themen noch Schwierigkeiten haben, findest du auf unserer Seite nützliche Informationen und kannst dir natürlich kostenlos so viele Übungsaufgaben ausdrucken wie du rechnen kannst.

Dividieren

Bei allen drei Methoden zur Bestimmung des ggT solltest du einfache Divisionsaufgaben lösen können

Schriftliches Dividieren und Dividieren mit Rest benötigst du für den Euklidischen Algorithmus (letzte Methode)
Über unseren Blogartikel zur schriftlichen Division kannst du dein Wissen wieder auffrischen und findest relevante Übungen zu dem Thema

Teilbarkeitsregeln

Du kannst mit Hilfe der Teilbarkeitsregeln schnell erkennen, ob eine Zahl durch z.B. 2;3;4;5;9;10 teilbar ist

Brauchst du eine Auffrischung? Dann schau dir Die wichtigsten Teilbarkeitsregeln nochmal an

Teilermengen

Für die Anwendung der ersten Rechenvorschrift GGT mit Hilfe von Teilermengen - Kochrezept 1 solltest du Teilermengen bilden können

Denke daran, dass du zum Bilden der Teilermenge nicht für alle Zahlen die Probedivision durchführen musst
Falls du eine Auffrischung benötigst findest du Im Artikel Primfaktorzerlegung eine Erklärung dazu

Primfaktorzerlegung

Die zweite Methode basiert auf der Primfaktorzerlegung

Wie die Primfaktorzerlegung funktioniert kannst du im Artikel Primfaktorzerlegung nachlesen

GGT mit Hilfe von Teilermengen - Kochrezept 1

Der größte gemeinsame Teiler zweier natürlicher Zahlen $a, b$ lässt sich mit Hilfe ihrer Teilermengen bestimmen. Auch wenn dieses Verfahren für große Zahlen zunehmend ineffizienter wird, ist diese Rechenvorschrift ein intuitiver Zugang, um sich mit dem abstrakten Konzept des ggT vertraut zu machen.

Wir erklären das Vorgehen Schritt für Schritt anhand des Beispiels $a=174$ und $b=116$ .

Schritt 1: Bilde die erste Teilermenge👈

Wir starten mit der Bestimmung der Teilermenge für die erste natürliche Zahl $a=174$ :

T_{174} = \{1;2;3;6;29;58;87;174\}

Mit Hilfe der wichtigsten Teilbarkeitsregeln ist die Teilermenge schnell bestimmt. Beachte, dass du zur Bestimmung der Teilermenge die Probedivision nur bis maximal $ \sqrt 174 \sim 13$ durchführen musst. Falls du eine Auffrischung hierzu brauchst, liest dir unseren Artikel zur Probedivision durch.

Schritt 2: Bilde die zweite Teilermenge 👈

Im zweiten Schritt verfahren wir mit $b=116$ analog wie in Schritt 1 und bestimmen die Teilermenge:

T_{116} = \{1;2;4;29;58;116\}

Schritt 3: Gemeinsame Teilermenge bilden 👈

Nun bildest du aus den beiden vorherigen Schritten die Schnittmenge der jeweiligen Teilermengen

\begin{aligned} T_{174\cap116} &=& \{\color{green}{1};\color{green}{2};3;6;\color{green}{29};\color{green}{58};87;174\} \cap \{\color{green}{1};\color{green}{2};4;\color{green}{29};\color{green}{58};116\}\\ &=& \{1;2;29;58\} \end{aligned}

Wenn du beide Mengen untereinander schreibst oder gemeinsame Teiler farblich markierst, kannst du die Schnittmenge einfach ablesen.

Schritt 4: ggT ablesen 👈

Der letzte Schritt ist dann nur noch das Maximum (also die größte Zahl) aus der Schnittmenge abzulesen. Wenn du die Schnittmenge der Größe nach aufsteigend sortiert hast, ist es die letzte Zahl in der Schnittmenge.

ggT(174,116) = 58

GGT mit Hilfe der Primfaktorzerlegung - Kochrezept 2

Die Primfaktorzerlegung ist eine zweite Methode mit deren Hilfe du ebenfalls den größten gemeinsamen Teiler zweier natürlicher Zahlen bestimmen kannst. Wir schauen uns dazu das gleiche Beispiel aus Methode 1 an, um Schritt für Schritt die Rechenvorschrift zu erklären:

Schritt 1: Erstelle die Primfaktorzerlegung für beide natürliche Zahlen 👈

Das Ergebnis der Primfaktorzerlegung für $a=174$ und $b=116$ schreibst du am Besten direkt untereinander.

Schritt1 zur Bestimmung des GGT mit Hilfe der Primfaktorzerlegung

Schritt 2: Gemeinsame Primfaktoren identifizieren 👈

Um den ggT zu erhalten, musst du nun alle Primfaktoren bestimmen, die sowohl Teil der Primfaktorzerlegung von $174$ als auch von $116$ sind.

Schritt2 zur Bestimmung des GGT mit Hilfe der Primfaktorzerlegung

Schritt 3: Primfaktoren multiplizieren 👈

Die gefundenen gemeinsamen Primfaktoren werden nun miteinander multipliziert und liefern den gesuchten größten gemeinsamen Teiler.

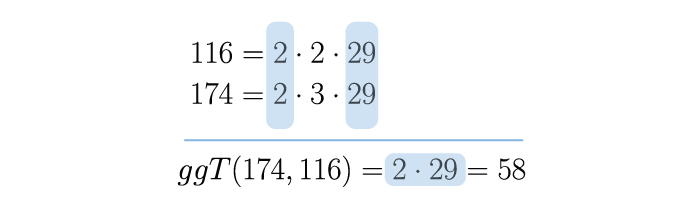
Schritt3 zur Bestimmung des GGT mit Hilfe der Primfaktorzerlegung

Achte darauf, dass du die Vielfachheit der Primfaktoren berücksichtigst. Kommt ein Primfaktor in beiden natürlichen Zahlen mehrfach vor, so muss dieser Primfaktor für die Bestimmung des größten gemeinsamen Teilers auch mehrfach multipliziert werden.

GGT mit Hilfe des Euklidischen Algorithmus - Kochrezept 3

Die beiden zuvor vorgestellten Rechenverfahren eignen sich nur solange die beiden natürlichen Zahlen, für die ein größter gemeinsamer Teiler gesucht wird, nicht zu groß sind. In solchen Fällen ist der Euklidische Algorithmus gegenüber der Primfaktorzerlegung sowie der Bestimmung durch Teilermengen vorzuziehen. Dabei macht sich der Euklidische Algorithmus folgende Eigenschaft zu Nutze

ggT(a, m\cdot a + b) = ggT(a,b)

indem die rekursive Anwendung der obigen Gleichung solange durchgeführt wird, bis sich der finale Term $ggT(a,b)$ nicht weiter reduzieren lässt. Damit vereinfacht sich das Problem, darauf eine endliche Anzahl an Divisionen durchzuführen, was insbesondere für Computer keine große Herausforderung darstellt. Wir erklären das Verfahren an dem konkreten Beispiel $ggT(7488, 4095)$ :

Schritt 1: Modulo-Berechnung der natürlichen Zahlen 👈

Führe in der ersten Zeile die Division mit den beiden natürlichen Zahlen aus der Aufgabenstellung durch. Dabei wird die größere Zahl durch die kleinere geteilt.

Schritt1 zur Bestimmung des GGT mit Hilfe des Euklidischen Algorithmus

Notiere auch den Rest der Divisionsaufgabe, da dieser im nächsten Schritt benötigt wird.

Schritt 2: Vereinfachte ggT-Aufgabe bestimmen 👈

Aus den Ergebnissen aus Schritt 1 und mit Hilfe der rekursiven Formel oben, ergibt sich nun eine ggT-Aufgabe mit zwei neuen natürliche Zahlen. Zum einen die kleinere Zahl der ursprünglichen ggT-Aufgabe und zum anderen der Rest der Divisionsaufgabe.

Schritt2 zur Bestimmung des GGT mit Hilfe des Euklidischen Algorithmus

Dazu schreiben wir in unserem Beispiel $4095$ in die nächste Zeile fort (in hellblau markiert) und teilen nun durch $3393$ , dem Rest der vorherigen Divisionsaufgabe (in lila markiert).

Schritt 3: Vereinfachte ggT-Aufgabe bestimmen (1. Iteration) 👈

Die Division ergibt wieder einen Rest verschieden von Null, so dass wir die nächste ggT-Aufgabe wie in Schritt 2 bestimmen können.

Schritt3 zur Bestimmung des GGT mit Hilfe des Euklidischen Algorithmus

Der Dividend $3393$ wird nun in die 3. Zeile fortgeschrieben (in hellblau markiert) und durch den Rest der vorherigen Divisionsaufgabe $702$ geteilt (in lila markiert).

Schritt 4: Vereinfachte ggT-Aufgabe bestimmen (2. Iteration) 👈

Wir wiederholen nun Schritt 2 bzw. Schritt 3 solange die Divisionsaufgabe keinen Rest zurück liefert.

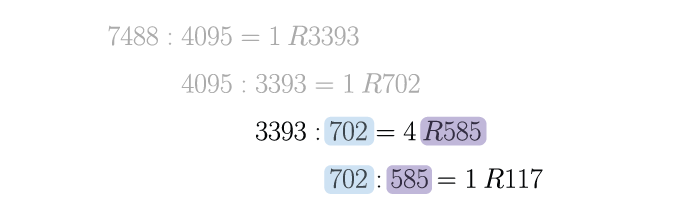
Schritt4 zur Bestimmung des GGT mit Hilfe des Euklidischen Algorithmus

Schritt 5: Vereinfachte ggT-Aufgabe bestimmen (letzte Iteration) 👈

Die letzte Iterationsschleife formuliert eine Divisionsaufgabe die keinen Rest hat (bzw. den Rest Null).

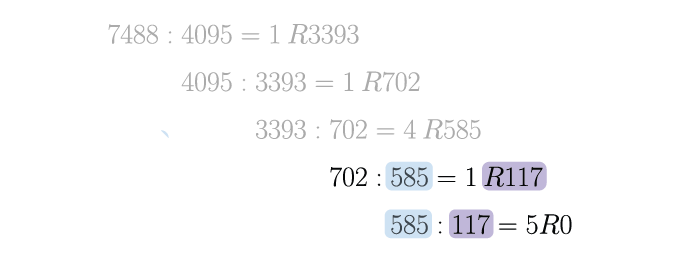
Schritt5 zur Bestimmung des GGT mit Hilfe des Euklidischen Algorithmus

Damit sind wir am Ende des Algorithmus angelegt und können das Ergebnis in der letzten Zeile ablesen.

Schritt 6: Ergebnis ablesen 👈

Das Ergebnis der ursprünglichen Aufgaben kann mit der letzten Zeile anhand des Divisors abgelesen werden.

Schritt6 zur Bestimmung des GGT mit Hilfe des Euklidischen Algorithmus

Somit ergibt $ggT(7488,40958) = 117$ .

Größter gemeinsamer Teiler für mehrere Zahlen 🚀

Für die Aufgabe, einen größten gemeinsamen Teiler für mehr als zwei natürliche Zahlen zu finden, können wir die Methoden, die wir in diesem Kapitel vorgestellt haben, anwenden. Da folgendes für den größten gemeinsamen Teiler gilt

\begin{aligned} ggT(a,b,c) &= ggT(a,ggT(b,c)) = \\ ggT(ggT(a,b),c) &= ggT(ggT(a,c),b) \end{aligned}

besteht die Aufgabe also darin, die Bestimmung des ggT mehrfach durchzuführen, wobei die Reihenfolge der Bestimmung dabei keine Rolle spielt.

Würden wir z.B. die Aufgabe bekommen, den ggT der drei natürlichen Zahlen $108;236,380$ zu bestimmen, könnten wir zuerst

ggT(108,236)=4

wie gehabt berechnen, um im Anschluss das Ergebnis dieser Berechnung für die zweite Bestimmung

ggT(4,380)=4

zu verwenden. Damit ist

ggT(108,236,380)=4

Teilermengen bestimmen

Falls du eine Auffrischung benötigst wie Teilermengen gebildet werden, dann schau dir unser Video dazu an

Fragen und Antworten

Was ist der größte gemeinsame Teiler einer Zahl und Null?

Der größte gemeinsame Teiler einer natürlichen Zahl a mit der Null ist der Betrag von a,

ggT(a,0) = |a|

Was ist der größte gemeinsame Teiler einer Zahl und 1?

Der größte gemeinsame Teiler einer natürlichen Zahl a mit 1 ist 1,

ggT(a,1) = 1

Wozu benötige ich den größten gemeinsamen Teiler?

Der ggT ist insbesondere bei der Vereinfachung von Brüchen, insbesondere beim systematischen Kürzen von Brüchen, sehr nützlich.

Wie bestimme ich den größten gemeinsamen Teiler?

Für die Bestimmung des ggT gibt es verschiedene Verfahren, wobei das Teilermengen-Verfahren, die Primfaktorzerlegung, sowie der Euklidische Algorithmus gängige Methoden hierfür sind.

Wie bestimme ich den ggT von drei Zahlen?

Bei der Bestimmung von

ggT(a_1,a_2,a_3)

verwenden wir die gleichen Methoden wie bei der Bestimmung des ggT von zwei Zahlen. Zuerst sucht man sich zwei der drei Zahlen aus, für die im ersten Schritt eine ggT-Bestimmung durchgeführt werden soll

ggT(a_1,a_2) = b

. Das Ergebnis der ersten Bestimmung wird dann als Zahl zusammen mit der dritten Zahl aus der ursprünglichen Aufgabenstellung verwendet und nochmals eine ggT-Bestimmung durchgeführt

ggT(a_3,b) = c

, wobei

c

das Endergebnis liefert.

Wann wird das Thema größter gemeinsamer Teiler in der Schule behandelt?

Der ggT wird in Deutschland typischerweise auf den weiterführenden Schulen (wie Gymnasium, Real- und Hauptschule) zwischen der 5. und 6. Klasse behandelt.

Mehr zu natürlichen Zahlen

Du suchst detailierte Informationen, wie zum Beispiel alle Teiler oder die Vielfachenmenge, zu einer bestimmten natürlichen Zahl? Dann wirst du hier fündig.

1-20

21-40

41-60

61-80

81-100

101-120

121-140

141-160

161-180

181-200

Größter gemeinsamer Teiler (ggT) - leicht erklärt

Größter gemeinsamer Teiler - Worum geht’s?