Primfaktorzerlegung - einfach erklärt

Stefan Vickers·09.05.2023

Primzahlen und die Primfaktorzerlegung im Speziellen sind ein unglaublich spannendes und auch aktuelles Thema, da Primzahlen ganz bestimmte Eigenschaften besitzen, die sich sehr gut für konkrete Anwendungen im Alltag gebrauchen lassen. Solltet ihr also auch zu der Sorte Mensch gehören, die sich gerne die Frage stellen: “Wozu brauch ich das 🤔?”, dann hält das Ende des Artikels eine Antwort für euch bereit.

Aber eins nach dem anderen. Wir starten den Blog mit einer Zusammenfassung der wichtigsten Informationen, die du rund um das Thema benötigst. Anschließend machen wir dich fit für das Lösen von typischen Übungsaufgaben und zeigen dir in welchem Kontext dir die Primfaktorzerlegung später wieder begegnen wird.

Bist du nicht auf der Suche nach Erklärungen, sondern nach Aufgaben zum Üben? Dann springe gleich zu unserem Aufgabengenerator und drucke dir kostenlos so viele Übungsblätter als PDF 📃 aus wie du rechnen kannst.

Primfaktorzerlegung - Worum geht’s 🤓?

Um zu verstehen worum es bei der Primfaktorzerlegung geht, solltest du zuallererst verstehen was eine Primzahl ist:

Primzahlen sind alle natürlichen Zahlen, die durch genau zwei Zahlen, nämlich durch $1$ und sich selbst, teilbar sind. Die kleinsten Vertreter dieser Spezies sind $2;3;5;7;11;$ usw. Natürliche Zahlen, die mehr als zwei Teiler haben, nennt man gemischte Zahlen.

Anhand dieser Definition sind sowohl die Null als auch die $1$ keine Primzahlen (eine Erklärung warum das so ist findest du im Abschnitt Fragen & Antworten). Zudem kann die Mathematik beweisen, dass sich jede gemischte Zahl in ein Produkt zerlegen lässt, welches ausschließlich aus Primzahlen besteht. Damit das nicht zu theoretisch wird, hier ein Beispiel:

\begin{aligned} 210 = 2\cdot3\cdot5\cdot7\cdot11 \end{aligned}

Auf der linken Seite der Gleichung steht mit $210$ eine gemischte Zahl und auf der rechten Seite mit $2;3;5;7;11$ ausschließlich Primzahlen.

Die Aufgabe eine natürliche Zahl in seine nicht mehr teilbaren “Bestandteile” (Primzahlen) zu zerlegen, nennt man dann Primfaktorzerlegung oder manchmal auch Faktorisierungsproblem (Problem eher im Sinne einer Herausforderung als ein Problem über das man sprechen müsste 😟).

Den Zusammenhang zwischen Primzahlen und gemischten Zahlen kann man sich ähnlich vorstellen, wie sich Atome zu Materie verhalten. Atom, aus dem griechischen atomos, bedeutet unteilbar und Atome (zusammen mit anderen Elementarteilchen) galten lange Zeit in der Physik als die kleinsten Bausteine aus denen unsere Materie zusammengesetzt ist ﹣ ähnlich wie die gemischten Zahlen aus “unteilbaren” Primzahlen zusammengesetzt sind.

Analogie der Primfaktorzerlegung bzgl. Atome und Materie

Voraussetzungen - Das solltest du können

Folgendes Vorwissen solltest du bereits mitbringen, um die Primfaktorzerlegung sicher zu meistern. Solltest du mit einem der Themen noch Schwierigkeiten haben, findest du auf unserer Seite nützliche Informationen dazu und kannst über unseren Aufgabengenerator kostenlos Übungsaufgaben zu den Themen ausdrucken.

Primzahlen

Du weißt was eine Primzahl ist und kannst bestimmen ob eine natürliche Zahl eine Primzahl ist

Die gängigsten Primzahlen kennst du sicher. Falls du doch mal nicht sicher sein solltest, kannst du bei den Primzahlen bis 100 im Abschnitt Hilfestellungen nachschauen

Teilbarkeitsregeln

Du kannst mit Hilfe der Teilbarkeitsregeln schnell erkennen, ob eine Zahl durch z.B. 2;3;4;5;9;10 teilbar ist

Brauchst du eine Auffrischung? Dann schau dir Die wichtigsten Teilbarkeitsregeln im Abschnitt Hilfestellungen noch mal an

Dividieren und Multiplizieren im Kopf

Die Primfaktorzerlegung fällt dir wesentlich leichter wenn du bereits sicher im Kopf dividieren und multiplizieren kannst

Da Kopfrechnen für viele Aufgaben nützlich ist, kann es Sinn machen Übungen dazu immer wieder beim Lernen mit einzubauen

Wurzelziehen (optional)

Wurzelziehen ist nicht zwingend erforderlich, kann aber beim Lösen von schwierigen Übungsaufgaben durchaus hilfreich sein

Mach dir aber keine Sorgen, wenn das Thema noch nicht in der Schule behandelt wurde. Wir kommen grundsätzlich auch ohne Wurzelziehen aus

Potenzschreibweise (optional)

Auch die Potenzschreibweise ist nicht zwingend erforderlich, allerdings erlaubt sie uns das Endergebnis der Primfaktorzerlegung am Ende etwas zu vereinfachen

Wenn Potenzen noch nicht in der Schule behandelt wurden, kannst du den letzten Vereinfachungschritt aber auch weglassen

Die Primfaktorzerlegung in Tabellenform | Ein Kochrezept 🚀

Zerlege die Zahl 126 in seine Primfaktoren! Eine typische Aufgabe, wie sie jedes Jahr von Millionen von Schülern in Deutschland gelöst werden muss 😀. Aber wie genau geht man hier vor? Zum Glück gibt es für die Primfaktorzerlegung eine Rechenvorschrift, die wir anhand des folgenden Beispiels Schritt-für-Schritt durchgehen können

Aufgabenstellung zur Primfaktorzerlegung anhand der Abspaltung des kleinsten Primfaktors

Schritt 1: Kleinste, teilbare Primzahl finden 👈

Falls die zu zerlegende natürliche Zahl, also in unserem Beispiel $126$ nicht bereits selbst eine Primzahl ist, muss diese durch eine andere Primzahl teilbar sein.

Schritt 1 - Primfaktorzerlegung anhand der Abspaltung des kleinsten Primfaktors

Dazu prüfst du die Teilbarkeit aller in Frage kommenden Primzahlen, wobei wir mit der kleinsten Primzahl $2$ starten und uns der Reihe nach über $3;5;7;11$ vorarbeiten. Warum du nicht bis $126$ sondern nur bis maximal $11$ prüfen musst, kannst du im Abschnitt Primzahltest - die Probedivision nachlesen.

Du hast Glück. $126$ ist durch $2$ teilbar und du bist bereits an dieser Stelle mit dem ersten Schritt fertig.

Schritt 2: Die erste Primzahl abspalten 👈

Wie bereits im Bild angedeutet, macht es insbesondere für Anfänger Sinn, die einzelnen Schritte in Tabellenform aufzuschreiben. In der ersten Spalte notierst du die gefundenen Primfaktoren. Die zweite Spalte kannst du für Zwischenschritte verwenden.

Den ersten Primfaktor aus Schritt 1 schreibst du also in die erste Spalte der nächsten Zeile (im Bild hellblau markiert).

Das Ergebnis der ersten Abspaltung $126 : 2 = 63$ kommt in die zweite Spalte der nächsten Zeile (im Bild lila markiert).

Schritt 3: Wiederhole Schritt 1 👈

Nun musst du die kleinste, teilbare Primzahl für die $63$ finden, wobei diesmal nur Primzahlen bis $7$ geprüft werden müssen.

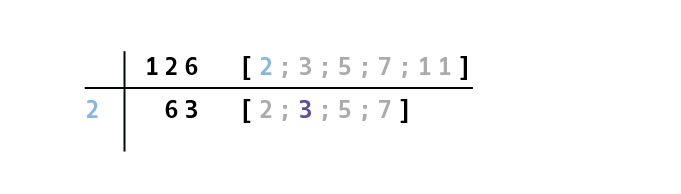
Schritt 3 - Primfaktorzerlegung anhand der Abspaltung des kleinsten Primfaktors

$63$ ist nicht durch $2$ teilbar, dafür aber durch $3$ .

Schritt 4: Wiederhole Schritt 2 und Schritt 3👈

Die $3$ ist der nächste Primfaktor und kommt somit in die erste Spalte der nächsten Zeile (in hellblau markiert). Das Ergebnis der Abspaltung $ 63 : 3 = 21 $ kommt in die zweite Spalte

Schritt 4 - Primfaktorzerlegung anhand der Abspaltung des kleinsten Primfaktors

Die zu prüfenden Primzahlen für die $21$ sind $2$ und $3$ , wobei wiederum nur die $3$ ein Teiler ist

Schritt 5: Wiederhole Schritt 2 und Schritt 3 [Iteration] 👈

Nun musst du Schritt 2 und Schritt 3 solange wiederholen, bis das Ergebnis der Abspaltung selbst eine Primzahl ist.

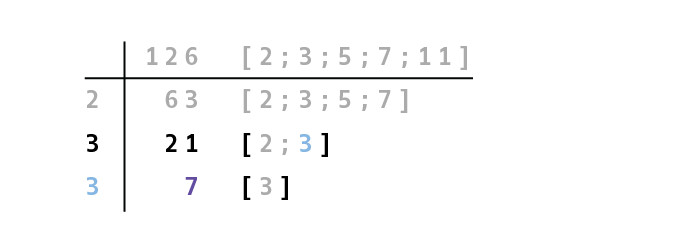
Schritt 5 - Primfaktorzerlegung anhand der Abspaltung des kleinsten Primfaktors

In unserem Beispiel ist das bereits in der nächsten Zeile der Fall, da $7$ eine Primzahl ist.

Schritt 6: Letzten Primfaktor ermitteln 👈

Da die $7$ selbst Teil der Primfaktorzerlegung ist, musst du auch die $7$ noch als Primfaktor in der ersten Spalte festhalten (wieder in hellblau markiert).

Schritt 6 - Primfaktorzerlegung anhand der Abspaltung des kleinsten Primfaktors

Der Vollständigkeit halber kannst du das Ergebnis der Abspaltung $7 : 7 = 1$ gerne aufschreiben (auch wenn dieser letzte Schritt immer das gleiche Ergebnis liefern sollte 😉)

Schritt 7: Ergebnis zusammenfassen 👈

Du hast nun alle Primfaktoren ermittelt und in die erste Spalte der Tabelle geschrieben. Um das Ergebnis zusammenfassen, schreibst du unter die Tabelle die Primfaktoren noch als Produkt auf.

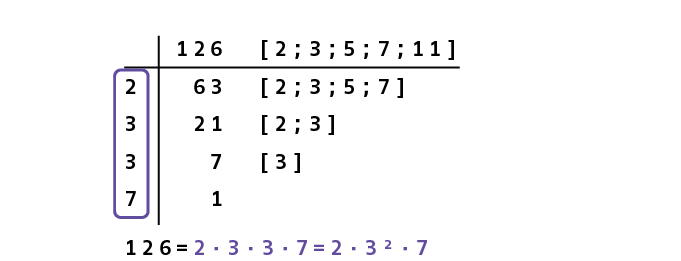
Schritt 7 und Lösung - Primfaktorzerlegung anhand der Abspaltung des kleinsten Primfaktors

Profi-Tipp: Wenn du die Potenzschreibweise bereits kennst, kannst du noch das Ergebnis in manchen Fällen (wie in unserem Beispiel) weiter zusammenfassen, indem du Produkte in die Potenzschreibweise vereinfachst.

Primfaktorzerlegung bei großen Zahlen - Wenn’s ein bisschen mehr sein darf 🔥

Der oben beschrieben Algorithmus zur Lösung der Primfaktorzerlegung kann immer durchgeführt werden und führt zu einem richtigen Ergebnis. Allerdings gibt es Situationen, in denen andere Verfahren entweder schneller oder auch leichter zum gewünschten Ziel führen. Dies kann insbesondere bei der Zerlegung von großen Zahlen der Fall sein.

Anstatt der Reihe nach immer den kleinsten Primfaktor abzuspalten, suchen wir uns nun einen beliebigen Teiler, der weder klein noch eine Primzahl sein muss, aber zu einer für uns einfachen Rechnung führt. Wir zerlegen die Zahl $1640$ .

Einfache Teiler finden 👈

Da du nun die Freiheit hast, mit einem beliebigen Teiler zu starten, bietet sich in unserem Beispiel die $10$ als Teiler an, da die Division mit der $10$ recht einfach ist. Dadurch wird $1640$ in $ 10 \cdot 164 = 1640$ zerlegt.

Schritt 1 - Primfaktorzerlegung anhand der Abspaltung von Teilern

Der Lösungsweg wird typischerweise in eine Baumstruktur dargestellt, indem du, ausgehend von der $1640$ , die beiden “Verästelungen” wie im Bild in Richtung $10$ und $164$ einzeichnest.

Teiler weiter zerlegen 👈

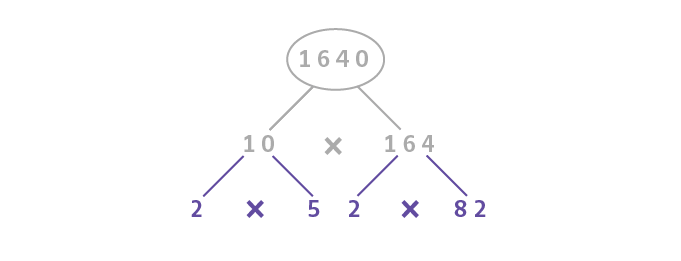
Schritt 2 - Primfaktorzerlegung anhand der Abspaltung von Teilern

Da wir im 1. Schritt die Teiler frei wählen durften, kannst du nun im 2. Schritt nicht mehr davon ausgehen, dass die gefundenen Teiler zwangsläufig Primzahlen sind. Das bedeutet, dass alle Teiler eventuell weiter zerlegt werden müssen.

Die $10$ lässt sich in $2\cdot 5$ zerlegen und $164$ in $2\cdot 82$ . Diese Zerlegung schreibst du als weitere Verästelung fort.

Wiederhole Schritt 2 👈

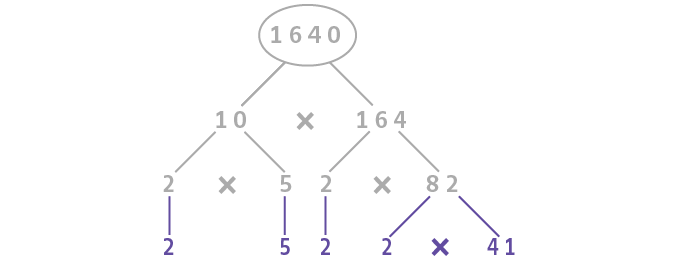
Schritt 3 - Primfaktorzerlegung anhand der Abspaltung von Teilern

Zu guter Letzt wiederholst du Schritt 2, bis sich alle gefundenen Teiler nicht weiter zerlegen lassen, also Primzahlen sind.

Achtung: In unserem Beispiel hattest du das für den linken Teil der Baumstruktur (unterhalb der $10$ ) bereits auf der 2. Ebene erreicht. Um später jedoch alle Primfaktoren zu erkennen, bietet es sich an, die Primzahlen mit einem einfachen geraden Strich auf die nächste Ebene fortzuführen.

Die Lösung der Aufgabe kannst du nun einfach anhand der letzten Ebene ablesen $2\cdot5\cdot2\cdot2\cdot41 = 2^{3}\cdot5\cdot41$ .

Primzahltest - die Probedivision

Für die Primfaktorzerlegung müssen wir bestimmen können, ob eine Zahl bereits eine Primzahl ist oder weiter zerlegt werden kann. In der Mathematik sind dazu zahlreiche Verfahren entwickelt worden wie z.B. der Fermatsche Primzahltest, das Sieb des Eratosthenes und viele andere. Im schulischen Kontext wird dies anhand der Probedivision überprüft, die für nicht zu große Zahlen einen vertretbaren Rechenaufwand mit sich bringt, aber gleichzeitig für die Schüler intuitiv zugänglich ist.

Bei der Probedivision wird überprüft, ob eine natürliche Zahl $n$ , sagen wir z.B. $137$ , durch eine Primzahl zwischen $2$ und $p_{max}$ , also in unserem Bsp. $2;3;5;7;11$ teilbar ist. Ist $n$ nicht durch eine dieser Primzahlen teilbar, ist $n$ selbst eine Primzahl.
Das interessante an diesem Verfahren ist, dass wir nicht alle Primzahlen bis $n$ , also $137$ prüfen müssen, sondern der Test bis $p = \lfloor \sqrt n \rfloor$ , also $\lfloor 11.7\rfloor = 11$ bereits ausreicht. Warum ist das so?

Wir starten mit der Annahme, dass die zu zerlegende Zahl $137$ eine Primzahl ist und überprüfen zuerst, ob sich $137$ durch eine Quadratzahl darstellen lässt. Mit etwas Übung erkennt man, dass $11^2=121$ kleiner, während $12^2=144$ bereits größer als $137$ ist. Damit kann $137$ keine Quadratzahl sein.

Wenn aber $137$ eine Primzahl ist, muss $137 = a\cdot b$ gelten, wobei nur vier verschiedene Konstellationen für $a, b$ möglich sind:

$a,b \gt 11$ : Da bereits $12^{2} \gt 137$ , kann diese Konstellation nicht zum gewünschten Ergebnis führen
$a,b \leq 11$ : Da bereits $11^{2} \lt 137$ , kann diese Konstellation ebenfalls nicht zum gewünschten Ergebnis führen
$a \leq 11$ und $b \gt 11$ : Diese Möglichkeit besteht in der Tat und muss anhand der Probedivision überprüft werden
$b \leq 11$ und $a \gt 11$ : Diese Konstellation ist aufgrund des Kommutativgesetzes identisch zur dritten Konstellation

Damit ist klar, dass es in einer möglichen Zerlegung von $137$ genau einer der beiden Faktoren kleiner $11$ sein muss. Wenn wir nun aber keinen Teiler kleiner $11$ finden, ist bewiesen, dass $137$ eine Primzahl ist.

Hilfestellungen

Die wichtigsten Teilbarkeitsregeln

Um Aufgaben zur Primfaktorzerlegung zügig zu lösen, sind die wichtigsten Teilbarkeitsregeln eine gute Hilfe

Eine Zahl ist durch $2$ teilbar, wenn ihre letzte Ziffer eine $0;2;4;6;8$ ist. Zahlen die durch $2$ teilbar sind, nennt man auch gerade Zahlen
Eine Zahl ist durch $3$ teilbar, wenn ihre Quersumme durch $3$ teilbar ist. Beispiel: Die Quersumme von $1371 = 1+3+7+1 = 12$ . Da $12$ durch $3$ teilbar ist, ist auch $1371$ durch $3$ teilbar
Eine Zahl ist durch $4$ teilbar, wenn ihre letzten beiden Ziffern durch $4$ teilbar ist. Beispiel: $24548$ ist durch $4$ teilbar, da $48$ durch $4$ teilbar ist
Eine Zahl ist durch $5$ teilbar, wenn ihre letzte Ziffer eine Null oder $5$ ist
Eine Zahl ist durch $6$ teilbar, wenn sie durch $2$ und $3$ teilbar ist
Eine Zahl ist durch $9$ teilbar, wenn ihre Quersumme durch $9$ teilbar ist
Eine Zahl ist durch $10$ teilbar, wenn ihre letzte Ziffer eine Null ist

Primzahlen bis 100

Um Aufgaben zur Primfaktorzerlegung schnell lösen zu können, ist es hilfreich, die Primzahlen bis 50 oder evtl. sogar bis 100 zügig zu erkennen. Falls du mal eine Primzahl vergessen haben solltest, dann kannst du sie hier nachschauen oder für dich ausdrucken 🧐

Häufige Fehler - Darauf solltest du achten

Die obere Grenze der Probedivision beachten ☝

Viele Schüler vergessen, dass sie bei der Probedivision nicht alle Primzahlen durchtesten müssen, sondern nur maximal bis zur Quadratwurzel der zu zerlegenden Zahl. Das kostet unnötig viel Zeit und Konzentration.

Beispiel: Wenn du bei der Probedivision von $89$ die Zahlen $2;3;5;7$ $\lt\left(\sqrt{89}\right)$ bereits getestet hast und keiner der Zahlen ein Teiler der $89$ ist, kannst du aufhören! Weitere Tests mit z.B. $11;13;17;$ usw. $\gt\left(\sqrt{89}\right)$ sind nicht mehr nötig, um zu zeigen, dass $89$ eine Primzahl ist.

Identische Primfaktoren falsch zusammenfassen ☝

Die gleiche Primzahl kann als Primfaktor einer zusammengesetzten Zahl mehrfach vorkommen. Man spricht dabei von der Vielfachheit eines Primfaktors. So hat z.B. die $2$ in der Primfaktorzerlegung von $8 = 2\cdot 2\cdot 2\cdot$ eine Vielfachheit von $3$ . Achte darauf, dass du die Primzahlen entsprechend ihrer Vielfachheit korrekt aufschreibst und nicht fälschlicherweise zusammenfasst.

Synonyme

Die Primfaktorzerlegung wird manchmal auch als Faktorisierungsproblem oder Faktorisierungsproblem für ganze Zahlen bezeichnet. Das Gegenteil einer Primzahl ist eine zusammengesetzte Zahl.

Beispiele für Primfaktorzerlegungen

Du brauchst noch mehr Beispiele für die Primfaktorzerlegung? Kein Problem, hier haben wir eine kleine Auswahl für dich zusammengestellt ✍️

Natürliche Zahl	Link
$36$	Primfaktorzerlegung 36
$100$	Primfaktorzerlegung 100
$210$	Primfaktorzerlegung 210
$225$	Primfaktorzerlegung 225
$2020$	Primfaktorzerlegung 2020
$2021$	Primfaktorzerlegung 2021
$2022$	Primfaktorzerlegung 2022

Verwandte Themen - Wozu brauche ich das eigentlich?

In der Schule

Die Primfaktorzerlegung solltest du in der Schule eher als Werkzeug betrachten, das dir dabei hilft andere Aufgaben leichter zu lösen. So wird typischerweise in der 5. Klasse über das Auffinden von groessten gemeinsamen Teilern (ggT) und kleinsten gemeinsamen Vielfachen (kgV) zweier Zahlen durch die Primfaktorzerlegung wesentlich einfacher. Ggt und kgV wiederum benötigst du für das Bruchrechnen (Addition, Subtraktion sowie das Kürzen von Brüchen), was dir sicherlich auch im Alltag bereits schon begegnet ist.

Die Anwendung - Primfaktorzerlegung in der Kryptographie

Stell dir vor, du möchtest jemandem eine Nachricht schicken, die ausschließlich für diese Person gedacht ist. Leider kann es aber immer passieren, dass ein dritter deine Nachricht abfängt und mitlesen möchte. Dieses Problem gab es bereits früher, als Nachrichten noch mit einem geschriebenen Zettel übermittelt worden sind, aber auch genauso in der heutigen Zeit, in der Nachrichten vor allem digital verschickt werden. Wenn du z.B. WhatsApp verwendest, um mit deinen Freunden zu chatten oder du über das Internet einkaufst und deine Bankdaten auf der Webseite des Shop Betreibers hinterlässt, hast du das gleiche Probleme wie früher ein römischer Feldherr der seinen Offizieren mitteilen musste wie Legionen zu verschieben sind: Wie verhindere ich, dass jemand der meine Nachricht abfängt (was du leider nie ausschließen kannst), diese lesen kann?

Um sich gegen solche Angriffe zu schützen, hast du die Möglichkeit, Nachrichten zu verschlüsseln. Das hört sich vielleicht kompliziert an, ist es im Prinzip aber gar nicht und lässt sich an einem sehr einfachen konkreten Beispiel demonstrieren:

Du schreibst einen geheimen Brief für einen Freund. Bevor du den Brief verschickst, solltest du diese Nachricht verschlüsseln, indem du alle Buchstaben um z.B. die nächsten drei Buchstaben im Alphabet verschiebst. Konkret bedeutet das: aus jedem A wird ein D, aus B wird E, aus C wird F, usw. Selbst wenn nun ein Spion deinen Brief abfangen sollte, ergeben die Wörter und Sätze in deinem Brief keinen Sinn mehr für ihn. Dein Freund jedoch kann die Geheimschrift wieder rückgängig machen (entschlüsseln), wenn du ihm zuvor mitgeteilt hast, um wie viele Stellen die Buchstaben verschoben wurden. Die Anzahl der Verschiebungen nennt man den geheime Schlüssel (zum ver- und entschlüsseln) der Nachricht.

Auch wenn moderne Verschlüsselungsverfahren wesentlich ausgefeilter sind als unser Beispiel, ist die Grundidee dennoch richtig.
Das Problem dieser Verschlüsselungstechnologie ist, dass du dem Empfänger den geheimen Schlüssel irgendwie mitteilen musst. Hat der “Spion” den Schlüssel während des Austauschs abfangen können, kann auch er jede Nachricht mitlesen und die Verschlüsselung ist nutzlos. Solche Verfahren nennt man symmetrische Verschlüsselung.

Asymmetrische Verschlüsselungen umgehen dieses Problem unter anderem mit Hilfe der Primfaktorzerlegung. Das Prinzip hierbei ist einfach. Beim Verschlüsseln einer Nachricht wird ein Schlüssel verwendet, der jedem bekannt sein darf (öffentlicher Schlüssel). Der Schlüssel für das Entschlüsseln einer Nachricht ist aber nur dem Empfänger bekannt (privater Schlüssel). Damit umgeht man das Problem, Schlüssel austauschen zu müssen.
Technisch macht man sich der Eigenschaft der Primfaktorzerlegung zur Nutze. Während das Erzeugen einer großen gemischten Zahl durch die Multiplikation zweier Primzahl für einen Computer trivial ist, ist die Aufgabe die gemischte Zahl wieder in seine Primfaktoren zu zerlegen selbst für Hochleistungsrechner nicht innerhalb einer vertretbaren Zeitspanne lösbar, wenn die Zahl groß genug ist. Diese Asymmetrie der Komplexität macht man sich zu Nutze, um öffentliche und private Schlüssel (die nicht geknackt werden können) zu generieren.

Wenn dich das Thema Kryptographie interessiert, dann schreib uns dazu über unser Kontaktformular. Wir nehmen gerne Themenwünsche für weitere Blog-Artikel auf. Ansonsten findest du natürlich auch einen guten Einstieg zur Kryptographie auf Wikipedia.

Fragen und Antworten

Ist die Null eine Primzahl?

Die Null ist per Definition keine Primzahl, da die Null nicht durch sich selbst teilbar ist.

Ist 1 eine Primzahl?

Die 1 ist keine Primzahl, weil man sie per Definition ausgeschlossen hat (eine Primzahl besitzt genau 2 Teiler, die 1 und sich selbst). Diese Definition wurde so gewählt, um gewisse Eigenschaften von Primzahlen, wie z.B. die Eindeutigkeit der Primfaktorzerlegung, zu erhalten.

Wie funktioniert die Primfaktorzerlegung?

Die Primfaktorzerlegung kann systematisch mit Hilfe der Probedivision durchgeführt werden. Dabei werden für die zu zerlegende Zahl so viele Teiler gesucht, bis alle Teiler und wiederum deren Teiler selbst nur noch Primzahlen sind.

Was bedeutet Primfaktorzerlegung?

Bei der Primfaktorzerlegung wird eine zusammengesetzte Zahl in das Produkt von ausschließlich Primfaktoren zerlegt. Dies ist immer möglich und auch eindeutig.

Wozu benötigt man die Primfaktorzerlegung?

Die Primfaktorzerlegung ist ein nützliches mathematisches Werkzeug welches bei der Suche des kleinsten gemeinsamen Vielfachen (kgV) und des größten gemeinsamen Teilers (ggT) zweier Zahlen nützlich und damit implizit relevant für die Bruchrechnung ist. Darüber hinaus finden Primzahlen und auch die Primfaktorzerlegung Anwendung in der Kryptographie (Verschlüsselungstechnologie).

Mehr zu natürlichen Zahlen

Du suchst detailierte Informationen, wie zum Beispiel alle Teiler oder die Vielfachenmenge, zu einer bestimmten natürlichen Zahl? Dann wirst du hier fündig.

1-20

21-40

41-60

61-80

81-100

101-120

121-140

141-160

161-180

181-200

Primfaktorzerlegung - einfach erklärt

Primfaktorzerlegung - Worum geht’s 🤓?