Schriftlich Multiplizieren einfach erklärt

Die schriftliche Multiplikation oder auch schriftlich “mal nehmen” genannt, ist eine Rechenvorschrift in der Mathematik, die immer dann zum Einsatz kommt, wenn uns das Multiplizieren im Kopf zu schwer fällt. Dabei funktioniert das schriftliche Multiplizieren glücklicherweise auch für vermeintlich komplexere Aufgaben, wie z.B. das Multiplizieren im Zahlenraum bis 100000 oder darüber hinaus, genauso wie das Multiplizieren mit kleinen zweistelligen Zahlen. In den nächsten Kapitel erklären wir dir alles was du zu diesem Thema wissen musst.
Bist du nicht auf der Suche nach Erklärungen sondern nach Aufgaben zum Üben? Dann springe gleich zu unserem Aufgabengenerator und drucke dir kostenlos soviel Übungsblätter als PDF 📃 aus wie du rechnen kannst.
Notwendiges Vorwissen
Folgendes Vorwissen solltest du bereits mitbringen, um die schriftliche Multiplikation sicher zu meistern. Solltest du mit einem der Themen noch Schwierigkeiten haben, findest du auf unserer Seite nützliche Informationen zu dem Thema und kannst dir natürlich kostenlos so viele Übungsaufgaben ausdrucken wie du rechnen kannst.
Kopfrechnen (kleines Einmaleins)
- Starte mit Kopfrechenaufgaben und Lösungen
Schriftliches Addieren (mit und ohne Übertrag)
- Aufgaben und Lösungen zur schriftlichen Addition
Das Kochrezept: So funktioniert die schriftliche Multiplikation 🚀
Im folgenden erklären wir dir Schritt-für-Schritt, wie du Aufgaben zur schriftlichen Multiplikation anhand eines einfachen Kochrezeptes lösen kannst. Zum Glück funktioniert das nahezu in allen Situationen 😋
Schritt 1: Die Aufgabe aufschreiben 👈
Schreibe die gesamte Multiplikationsaufgabe inklusive dem “=”-Zeichen am Ende der Aufgabe in eine Zeile. Um deine Rechenschritte von der eigentlichen Aufgabe zu trennen, machst du einen geraden Strich unterhalb der Aufgabe.
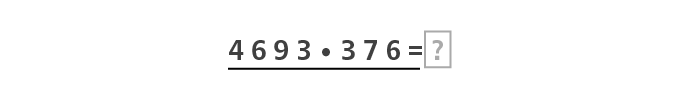
Schritt 2: Den größten Zahlenwert ausmultiplizieren 👈
Multipliziere nun den ersten Faktor (also 4693) schrittweise mit der Ziffer des zweiten Faktors, die den höchsten Stellenwert besitzt (also die 3).
Das Ergebnis muss direkt unterhalb des entsprechenden Stellenwerts geschrieben werden. Die Lücken unterhalb der anderen Stellenwerte bleiben entweder leer oder werden mit 0 aufgefüllt.
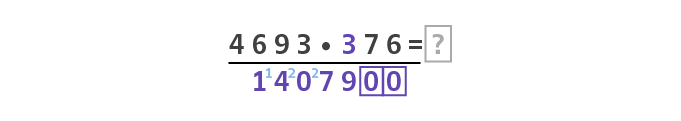
Achtung: In manchen Fällen musst du beim Multiplizieren einen Übertrag bilden, den wir in der Beispielrechnung für dich in hellblau markiert haben. Achte darauf, dass du den Übertrag aus versehen nicht als Ergebnis der Multiplikation aufschreibst.
Schritt 3: Nächsthöheren Zahlenwert ausmultiplizieren 👈
Nun multiplizierst du die Ziffer mit dem nächsthöheren Stellenwert, (also die 7) aus. Verfahre hierzu wie bei Schritt 2 und füge nun zusätzlich noch ein “±Zeichen” an den Anfang des Teilergebnisses.
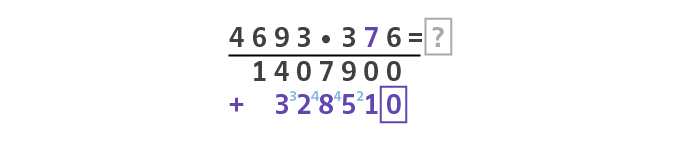
Achte wieder darauf, das du das Ergebnis unterhalb des entsprechenden Stellenwerts geschrieben hast und die Lücken entweder leer lässt oder mit 0 aufgefüllt hast.
Schritt 4: Wiederhole Schritt 3 👈
Wiederhole nun Schritt 3 für allen anderen Ziffern des zweiten Faktors (in unserem Beispiel bleibt nur noch die 6). Sobald du am Ende angekommen bist ziehst du einen geraden Strich unterhalb der Teilergebnisse.
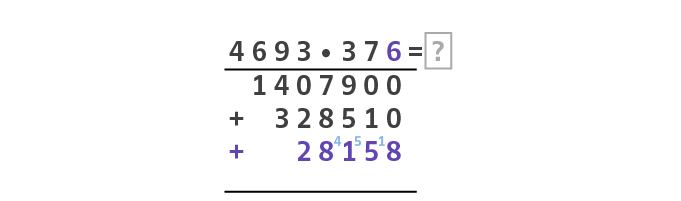
Achtung: Lass ein wenig Platz zwischen Teilergebnis und Strich, da du eventuell mit Übertrag rechnen musst.
Schritt 5: Teilergebnisse schriftlich addieren 👈
Führe nun die schriftliche Addition für die jeweiligen Teilergebnisse durch. Die Summe der Teilergebnisse ist auch gleichzeitig das Ergebnis der Multiplikation.
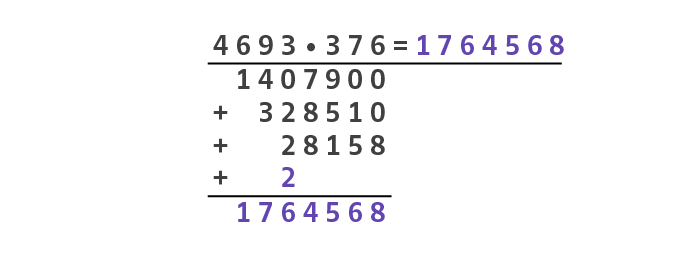
Dieses Kochrezept funktioniert für beliebige Multiplikationsaufgaben, solange wir uns im Zahlenraum der natürlichen, also der positiven ganzen Zahlen bewegen. Die Schwierigkeit bei Aufgaben mit großen Zahlen besteht dann vielmehr darin, die Rechenschritte sauber und ordentlich aufzuschreiben; die Rechenvorschrift selbst hingegen bleibt unverändert.
Für Aufgaben, die auch rationale Zahlen (also Zahlen mit Komma) einschließen, muss die Rechenvorschrift leicht modifiziert werden. Falls du dich für das schriftliche Multiplizieren mit “Komma” interessiert, dann findest unter Sonderfälle der schriftlichen Multiplikation entsprechende Erklärungen.
Schriftliche Multiplikation - anschaulich erklärt
Was kann man sich eigentlich unter der Rechenvorschrift, so wie wir sie oben definiert haben und wie sie unsere Kinder in der Schule lernen, vorstellen und warum liefert sie eigentlich das richtige Ergebnisse? Ein möglicher Zugang hierfür ist das Distributivgesetz, welches uns erlaubt die Aufgabe in einzelne Teile zu zerlegen und folgendermaßen umschreiben:
Durch einfache Umformungen der Aufgabe haben wir erreicht, dass sich die Multiplikationsaufgabe soweit vereinfacht, dass wir in einem ersten Schritt den ersten Faktor der Aufgabe (also 4693) nur noch mit Ziffern (also Zahlen im Zahlenraum bis 10) multiplizieren müssen. Das ist einfach und lässt sich im Kopf bewerkstelligen:
In einem zweiten Schritt müssen dann nur noch die Teilergebnisse mit entsprechenden Zehnerpotenzen multipliziert (mal 10, mal 100, …) werden und alle Teilergebnisse (schriftlich) addiert werden. Dieses Vorgehen zerlegt eine komplexe Aufgabe in viele leichtere Einzelaufgaben und lässt sich somit in einen Algorithmus überführen, den wir und unsere Kinder in der Schule lernen können.
Sonderfälle der schriftlichen Multiplikation
Die Rechenvorschrift zur schriftlichen Multiplikation ist für die meisten Aufgabentypen identisch. Das bedeutet unabhängig davon ob wir im Zahlenraum bis 100 oder bis 1.000.000 arbeiten, das Vorgehen bleibt das gleiche. Einige wenige Sonderfälle gibt es dennoch, wie z.B. das halbschriftliche Multiplizieren oder das schriftliche Multiplizieren von Dezimalzahlen.
Halbschriftliches Multiplizieren
Das halbschriftliche Rechnen wird im Mathematikunterricht vor allem in der 3. Klasse unterrichtet und dient mitunter zur Vorbereitung des schriftlichen Rechnens. Das halbschriftliche Rechnen wird in allen vier Grundrechenarten (Addieren, Subtrahieren, Dividieren und Multiplizieren) angewandt und unterscheidet sich gegenüber dem schriftlichen Rechnen darin, dass Lösungsstrategien nicht fest vorgegeben sind sondern vom Schüler frei gewählt werden. Dabei soll der Schüler die besondere Gegebenheiten der Aufgabenstellung berücksichtigen und selbst eine geeignete Strategie entwickeln, die ihm das Rechnen erleichtert. Im Gegensatz zum Kopfrechnen hingegen, werden beim halbschriftlichen Rechnen Zwischenrechnungen und Rechenschritte aufgeschrieben (siehe hierzu auch die Erklärungen des Deutschen Zentrums für Lehrerbildung).
Ein typisches Lösungsmuster des halbschriftlichen Multiplizieren ist der “Stellenweise” Lösungsansatz, bei dem die Faktoren in ihre Stellenwerte zerlegt und einzeln multipliziert werden.
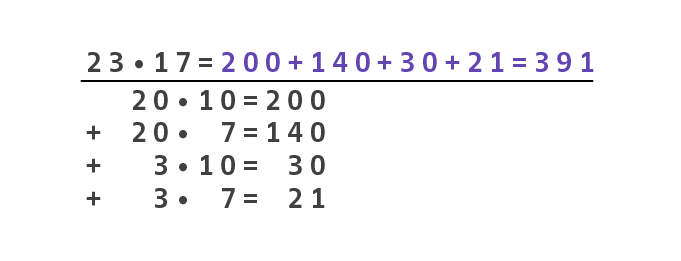
Andere Strategien, wie z.B. das “Schrittweise Verfahren”, das “Vereinfachen” oder auch die “Strategie der Hilfsaufgabe” sowie typisch Fehlerquellen findet ihr ebenfalls beim Deutschen Zentrum für Lehrerbildung.
Schriftliches Multiplizieren mit Nullstellen
Beinhaltet der zweite Faktor der Multiplikationsaufgabe eine Null in einem seiner Stellenwerte, wie z.B. 107 oder 3056, kann diese Konstellation insbesondere bei Anfängern noch zu Verwirrung führen. Dabei müssen wir auch in diesem Fall die Rechenvorschrift einfach konsequent anwenden, so dass das Multiplizieren des ersten Faktors mit der Null als Teilergebnis entsprechend Null zurück liefert.

Geübte Schüler können später auf das Teilergebnis Null verzichten, sollten jedoch im Anschluss daran darauf achten, dass die darauffolgenden Teilergebnisse unter den richtigen Stellenwert geschrieben wird.
Schriftlich Multiplizieren “mit Komma”
Um Dezimalzahlen (rationaler Zahlen oder Zahlen mit “Komma”) zu multiplizieren, müssen wir unsere Rechenstrategie nur minimal anpassen. Zu Beginn der Aufgabe tun wir so, als ob das “Komma” im ersten Faktor oder im zweiten Faktor oder evtl. sogar in beiden Faktoren (je nach Aufgabe) nicht existiert und führen die schriftliche Multiplikation wie gehabt aus.

Die erwähnte Modifikation erfolgt am Schluss der Rechnung und muss nur noch beim Endergebnis berücksichtigt werden. Dazu Zählen wir die Stellen des ersten und zweiten Faktors, um die das Komma jeweils nach rechts verschoben werden muss, damit es hinter der letzten Ziffer verschwindet.
- Zwei Stellen bei 46,93 um 4693 zu erhalten
- Eine Stelle bei 37,6 um 376 zu erhalten
Insgesamt mussten wir das Komma um drei (2+1) Stellen nach rechts verschieben, was wir nun beim Endergebnis wieder rückgängig machen und somit das Komma um drei Stellen nach links verschieben. Damit erhalten wir das Endergebnis

Typische Fehlerquellen - Darauf solltest du achten
Unsauberes Arbeiten
Bei der schriftlichen Multiplikation ist es besonders wichtig, dass du ordentlich arbeitest und die Teilergebnisse unter die richtigen Stellenwerte schreibst. Wenn du bereits an dieser Stelle unsauber arbeitest, kommt nur noch in den seltensten Fällen das richtige Ergebnis heraus.
Fehler beim Übertrag
Wenn du die Ziffern des zweiten Faktors mit dem ersten Faktor multiplizierst, musst du in manchen Fällen einen Übertrag bilden (z.B. bei
Einmaleins
Lass dir beim Einmaleins ruhig Zeit, um das richtige Ergebnis zu berechnen. Denke auch daran, dass eine Zahl, die mit Null multipliziert wird, im Ergebnis immer Null ergibt und nicht die Zahl selbst.
Wie sagt man noch zur Multiplikation?
Typische Synonyme, die im Zusammenhang mit der Multiplikation und somit auch möglicherweise für die schriftliche Multiplikation verwendet werden, sind:
- Mal nehmen,
- Das Produkt bilden,
- Vervielfachen,
- Verdoppeln (mal 2), verdreifachen (mal 3), …
- Um x erhöhen (wobei hier x für z.B. eine Zahl steht)
Sollte einer dieser Begriffe z.B. in einer Textaufgabe vorkommen, kann das bereits ein guter Hinweis darauf sein, was zu tun ist 😜.
Wenn du nach der Umkehraufgabe oder der Gegenoperation zur Multiplikation gefragt wirst, ist das die (schriftliche) Division. Mit der kannst du demzufolge auch immer die Probe machen um festzustellen, ob du richtig gerechnet hast.
Fallen dir noch weitere Synonyme ein? Dann schreib uns doch über unser Kontaktformular.
Schriftliche Multiplikation - Aufgaben mit Lösungen
Falls du gerne die schriftliche Multiplikation üben möchtest, dann hast du hier die Gelegenheit dir entweder bereits fertige Übungsblätter herunterzuladen, in unserem Aufgabengenerator eigene Übungsblätter zusammenzustellen oder direkt mit unserem Trainingscenter zu starten 🚀.