Schriftlich Multiplizieren einfach erklärt
Verstehe wie die schriftliche Multiplikation funktioniert und stelle dir individuelle Übungsblätter samt Lösungen zum Thema zusammen.
30.11.2023·Grundrechenarten erklärt
MathekönigDarstellung von Funktionen
Linus Haertel·09.05.2023
Es gibt mehrere Arten, wie man Funktionen ausdrücken kann. Wir werden im folgenden drei Darstellungsformen für Funktionen vorstellen. Nicht immer kann jede der Darstellungsmöglichkeiten für eine Funktion genutzt werden. Welche Darstellungsformen möglich und sinnvoll sind, hängt ganz von der Komplexität der Funktion ab.
Grundsätzlich bildet jede Funktion von der
Im Prinzip kannst du dir
Stattdessen wird meist eine der folgenden drei Darstellungen für eine Funktion genutzt:
Wertetabellen
Wertetabellen sind eine besonders einfache Form der Darstellung einer Funktion und bieten sich vor allem bei unkomplizierten Funktionen mit kleiner Definitionsmenge an. Ist die Definitionsmenge jedoch groß, funktioniert die Darstellung einer Funktion in Form einer Wertetabelle jedoch nicht mehr.
Beispiel Wertetabelle
Ein Beispiel für eine Wertetabelle ist:
| -5 | 1 |
| -2 | -3 |
| 0 | 4 |
| 3,5 | 2 |
| 6 | 13 |
| 8 | -1 |
Mehr Informationen zu Wertetabellen findest du hier.
Funktionsgleichung
Funktionsgleichungen geben, wie der Name schon sagt, eine Gleichung an, mit welcher zu jedem Element aus der Definitionsmenge das zugehörige Element aus der Wertemenge berechnet werden kann. Diese Form der Darstellung ist sehr beliebt, da eine einzige Gleichung ausreicht um die ganze Funktion zu definieren. Allerdings muss es erstmal möglich sein eine Funktion per Gleichung vollständig und korrekt zu charakterisieren. Nicht bei jeder Funktion ist dies möglich.
Beispiel Funktionsgleichung
Ein Beispiel für eine Funktionsgleichung ist:
Möchtest du mehr über Funktionsgleichungen erfahren? Hier findest du alles, was du über Funktionsgleichungen wissen musst.
Funktionsgraph
Ein Funktionsgraph beschreibt eine Funktion graphisch. Dies ist ziemlich cool, da man direkt auf den ersten Blick wichtige und interessante Eigenschaften der Funktion sieht. Funktionsgraphen kann man zudem relativ leicht erzeugen. Häufig lässt sich eine Wertetabelle in einen Funktionsgraphen überführen. Eine Funktionsgleichung lässt sich sogar immer auch als Funktionsgraph darstellen. Der Nachteil von Funktionsgraphen ist, dass man mit ihnen nicht wirklich rechnen kann. Man sieht viele Eigenschaften und kann auch wichtige Punkte auf dem Funktionsgraphen schnell grob bestimmen, allerdings ist es oft unmöglich exakte Informationen zu erhalten. Zudem ist es zwar leicht aus einer Funktionsgleichung einen Funktionsgraph zu erzeugen, umgekehrt geht dies jedoch nicht.
Beispiel Funktionsgraph
Ein Beispiel für einen Funktionsgraph ist:
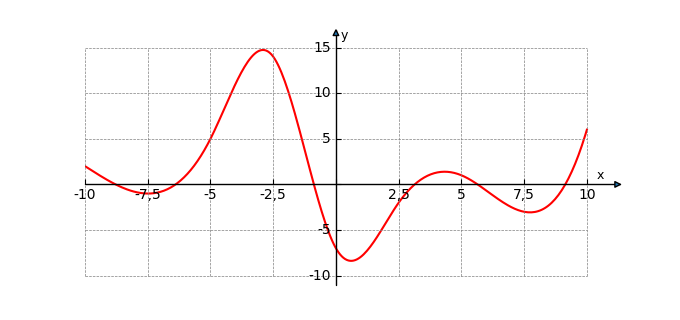
Einen umfassenden Artikel zu Funktionsgraphen findest du hier.
Funktionsgleichungen und Funktionsgraphen - Aufgaben mit Lösungen
Wenn du trainieren möchtest Funktionsgleichungen und Funktionsgraphen einander zuzuordnen, findest du hier passende Übungsaufgaben mit Lösungen zu unterschiedlichen Schwierigkeitsgraden.
Fragen und Antworten
Die drei beliebtesten Darstellungsformen einer Funktion sind:
Man nutzt Wertetabellen besonders dann um eine Funktion dar zu stellen, wenn die Definitionsmenge klein ist.
Nicht jede Funktion lässt sich durch eine Funktionsgleichung darstellen.
Es ist in der Regel schwierig genau Funktionswerte abzulesen.
Das könnte dich auch interessieren
