Schriftlich Multiplizieren einfach erklärt
Verstehe wie die schriftliche Multiplikation funktioniert und stelle dir individuelle Übungsblätter samt Lösungen zum Thema zusammen.
30.11.2023·Grundrechenarten erklärt
MathekönigDer Dreisatz in der Prozentrechnung
Anna Redenius·09.05.2023
Der Dreisatz ist eines der wichtigsten Tools in der Prozentrechnung, gerade wenn man ohne einen Taschenrechner arbeitet. Durch dieses Verfahren wird aus einer schwierigen Ein-Schritt-Rechnung eine deutlich einfachere Rechnung in Zwei Schritten.
Woher hat der Dreisatz seinen Namen?
Der Name des Dreisatzes kommt von den drei Schritten in denen man vorgeht, auch wenn nur zwei davon tatsächlich Rechenschritte sind.
- Schritt 1: Was hat man gegeben?
- Schritt 2: Wie viel sind 1%?
- Schritt 3: Wie groß ist der gesuchte Anteil?
Viele Rechnungen lassen sich so vereinfachen, so dass man sie auch ohne Taschenrechner leicht lösen kann.
Der Dreisatz lässt sich auf alle Rechnungen der Prozentrechnung anwenden.
Beispielrechnung
Wir wollen den Prozentwert für 7% von 40 bestimmen.
Schritt 1: Was ist gegeben?
Schritt 2: Wie viel sind 1%?
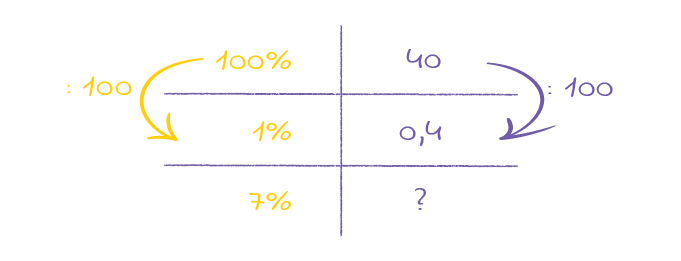
Schritt 3: Wie viel sind 7% von 40?
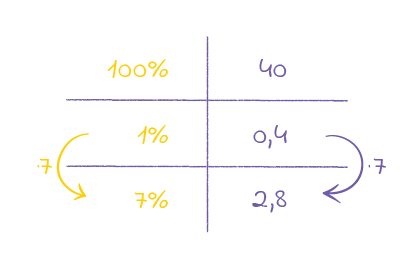
Damit ergeben sich 7% von 40 zu 2,8.
Intelligenter Dreisatz
Beim klassischen Dreisatz rechnet man zuerst den Wert für 1 Prozent aus, oft ist dies aber nicht der schnellste weg.
Beim intelligenten Dreisatz schaut man sich an, ob es gemeinsame Teiler zwischen gegebenem und gesuchtem Wert gibt.
Man rechnet im ersten Schritt somit nicht immer zwangsläufig den Wert für 1% aus.
Auch dieser Dreisatz kann in drei Schritten ausformuliert werden:
- Schritt 1: Gibt es gemeinsame Teiler zwischen gegebenem und gesuchtem Wert?
- Schritt 2: Passt einer dieser Teiler auch zum gegebenen Prozentwert?
- Schritt 3: Errechnen des Wertes mit dem Dreisatz über den gemeinsamen Teiler.
Dies klingt zunächst nicht sehr anschaulich, wird aber einfacher, wenn wir das Verfahren an einem Beispiel verdeutlichen.
Beispielrechnung
Man hat gegeben, dass 60% des Preises 24€ sind und soll nun errechnen, wie viel 25% des Preises wären. 24 ist nicht direkt durch 60 teilbar, beim “normalen” Dreisatz müssten wir also mit Kommazahlen rechnen. Hiermit würden wir zwar auch zum richtigen Ergebnis kommen, mit unserem intelligenten Dreisatz kommen wir aber schneller zum Ziel:
Schritt 1: gemeinsame Teiler bestimmen:
60 und 25 lassen sich beide durch 5 teilen. Es gibt also einen gemeinsamen Teiler, der nicht 1 ist. Dieser ist 5.
Schritt 2: passt dieser auch zum Prozentwert?
Um von 60% zu 5% zu gelangen, müssen wir durch 12 teilen. Der Prozentwert für 60% ist 24, was ebenfalls gut durch 12 teilbar ist.
Schritt 3: Dreisatz mit dem gemeinsamen Teiler
So haben wir eine komplizierte Rechnung schnell und einfach gelöst!
Aufgaben zum Üben
Du hast noch nicht genug vom Prozentwert? Dann gibt es hier weitere Aufgaben und Übungshilfen!
Das könnte dich auch interessieren
