Schriftlich Multiplizieren einfach erklärt
Verstehe wie die schriftliche Multiplikation funktioniert und stelle dir individuelle Übungsblätter samt Lösungen zum Thema zusammen.
30.11.2023·Grundrechenarten erklärt
MathekönigEinführung in die Prozentrechnung
Anna Redenius·09.05.2023
Wahrscheinlichkeiten, Verhältnisse und Veränderungen lassen sich alle besonders gut in Prozenten ausdrücken. Die Anteile an einem Ganzen werden hierbei in Hundertsteln dargestellt, das Ganze ist dabei immer 1 bzw. Hundert Prozent. Die Prozentrechnung hängt eng mit der Bruch- und der Dezimalrechnung zusammen.
Was bedeutet Prozent?
Prozent bedeutet “bezogen auf Hundert”, ein Prozent sind also gleichbedeutend mit einem Hundertstel. Der Begriff leitet sich vom italienischen “per cento” ab, was “von Hundert” bedeutet.
Ursprünglich wurde dies mit cto abgekürzt, hieraus entstand das heutige Prozentzeichen.
Welche Voraussetzungen gibt es für die Prozentrechnung?
Um ein Problem in Prozenten betrachten zu können muss man sich zunächst überlegen, auf welches Ganze man sich hier beziehen will, was also der Grundwert sein soll. Dieser Grundwert ist unsere Referenz und somit immer 100 %.
Des Weiteren müssen wir mit Größen arbeiten, von denen wir einen Anteil bestimmen können, z.B. 50%, dies ist unser Prozentsatz. Was ist damit gemeint? Man kann zum Beispiel sagen, dass eine Klasse zu 50% aus Menschen mit braunen Augen besteht, man kann jedoch nicht sagen, dass jemand zu 50% Vater ist. Man hat entweder Kinder oder man hat keine Kinder, dieser Zustand ist nicht weiter unterteilbar. Das zu betrachtende Problem muss also in Anteile aufteilbar sein.
Zu guter Letzt muss man diesen Anteil in der Einheit des Grundwertes auch bestimmen können. Diesen Anteil nennen wir den Prozentwert. Bei aufteilbaren Größen existiert eigentlich immer auch ein Prozentwert, manchmal kann die Umrechnung hier allerdings zu komischen Zwischenwerten führen.
Hierzu ein Beispiel. Im Durchschnitt sind ca 10 % aller Menschen Linkshänder, wenn wir diesen Prozentsatz jetzt auf eine Klasse mit 27 Schülern anwenden, 27 ist hier also der Grundwert, erhalten wir einen Prozentwert von 2,7 Schülern. “Schüler” ist jedoch eine Einheit, die sich schlecht in Kommazahlen ausdrücken lässt. Hier würde man im Normalfall auf 3 Schüler aufrunden.
Formeln der Prozentrechnung
Eine Ausführliche Herleitung dieser Gleichungen findest du im Artikel Formeln der Prozentrechnung. Hier sind einmal die wichtigsten Formeln zusammen gefasst:
Die Grundgleichung der Prozentrechnung:
Aus dieser Gleichung lassen sich alle anderen Gleichungen ableiten.
Den Grundwert berechnet man mittels:
Den Prozentwert über:
Und den Prozentsatz (als Prozentzahl) mit:
Als Merkhilfe kann hier auch das Dreieck der Prozentrechnung verwendet werden.
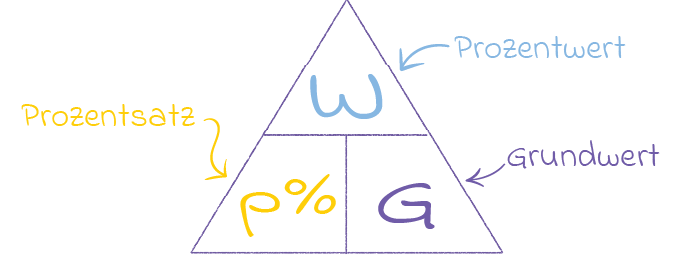
Was macht man damit eigentlich?
Im Artikel Prozentrechnung im Alltag werden einige Alltagsbeispiele durchgerechnet. Auch unter Prozent und Promille gibt es ein interessantes Rechenexperiment in Bezug auf Alkohol und Fahrtüchtigkeit.
An und für sich lässt sich die Prozentrechnung an allen Stellen nutzen, an denen Verhältnisse oder Veränderungen ausgedrückt werden.
Beispielrechnung: Wie viel Rand steckt in der Pizza?
Nehmen wir an, bei dir zuhause gibt es Pizza zum Mittag und du willst herausfinden, welchen Anteil der Rand an der Pizza hat.
Hierzu musst du zunächst den Durchmesser der Pizza bestimmen, beispielsweise
Die gesamte Pizza hat damit eine Fläche von:
Jetzt bleibt zu bestimmen, welchen Anteil der Rand (
Die Pizza besteht also zu fast 25% aus Rand. Im Artikel Darstellungsweisen der Prozentrechnung wird gezeigt, dass 25% einem Viertel entsprechen. Die Pizza besteht also fast zu einem Viertel aus Rand!
Übersicht
Hier haben wir alles wichtige nochmal für dich zusammengefasst!
Das könnte dich auch interessieren
