Lineare Gleichungen mit einer Variablen lösen, in denen die Variable einmal vorkommt

Schritt 1: Alle Summanden und Subtrahenden auf die Seite des Gleichheitszeichens bringen, wo x NICHT steht👈

In unserem Beispiel muss nur noch die “-5” auf die andere Seite gebracht werden. Die “+20” steht bereits auf der richtigen Seite, nämlich dort, wo $x$ nicht vorkommt.

Um die “-5” auf die andere Seite des Gleichheitszeichen zu bringen, führen wir eine Äquivalenzumformung durch. Nämlich addieren wir auf beiden Seiten der Gleichung “+5”:

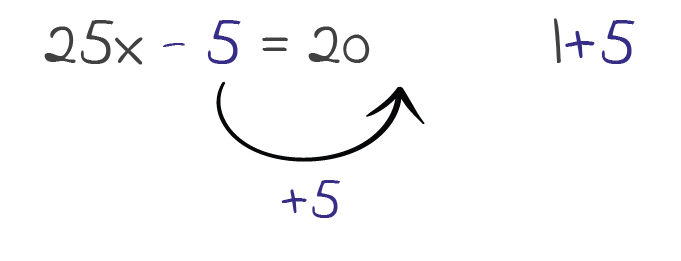
Schritt 2: Die Gleichung vereinfachen 👈

Wenn du später erfahrener im Umgang mit linearen Gleichungen bist, wirst du diesen Schritt wahrscheinlich automatisch machen und musst ihn so nicht explizit aufschreiben. Für den Anfang hilft es aber zu verstehen, was überhaupt passiert.

Auf beiden Seiten der Gleichung wurde “+5” addiert. Dies verrechnen wir nun mit den Zahlen, die schon vorher dort standen:

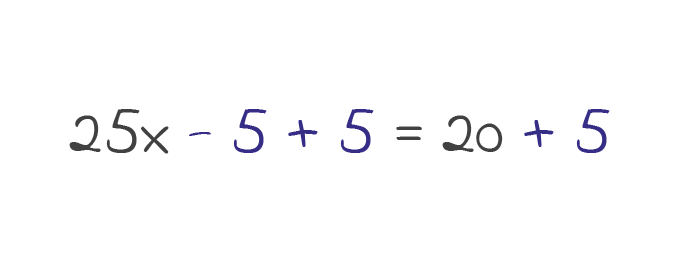
Auf der linken Seite der Gleichung steht nun “-5+5”. Dies ergibt offensichtlich Null und war ja gerade die Idee hinter der Operation “+5”. Das $x$ steht nun nämlich schon fast alleine auf der linken Seite der Gleichung:

Schritt 3: Durch Vorfaktor von x teilen 👈

Der Vorfaktor von $x$ ist die Zahl mit der $x$ multipliziert wird. Hier ist es also die Zahl “25”. Durch diese Zahl teilen wir nun beide Seiten der Gleichung damit $x$ vollständig isoliert steht:

Dies sieht dann so aus:

Schritt 4: Die Lösung aufschreiben 👈

Da wir durch den Vorfaktor von $x$ geteilt haben, steht $x$ nun mit Vorfaktor “1” auf der linken Seite der Gleichung. Die “1” lässt man weg, denn es gilt $1 \cdot x = x$. Unsere Variable $x$ ist damit vollständig isoliert. Nun müssen wir nur noch die rechte Seite der Gleichung ausrechnen und die Lösung notieren. Wir haben Glück und teilen auf der rechten Seite der Gleichung ebenfalls 25 durch 25. Damit haben wir die Lösung:

Schritt 5: Probe durchführen 👈

Als letztes führen wir eine Probe durch um sicher zu gehen, dass unsere Lösung richtig ist. Dazu setzen wir die von uns aus gerechnete Lösung $x=1$ in die ursprüngliche Gleichung $25 \cdot x -5 = 20$ ein:

Ausrechnen ergibt $20=20$, was eine wahre Aussage ist. Unsere Lösung stimmt also! 👍
Dieses Beispiel war ziemlich einfach, sollte dir aber das Vorgehen zum Lösen einer linearen Gleichung gezeigt haben. Jetzt bist du gefragt, zeige dein Wissen und löse lineare Gleichungen in unserem Aufgabengenerator.