Zahlen Runden

Stefan Vickers·09.05.2023

Beim Runden von Zahlen tolerieren wir Ungenauigkeit im Austausch für Vereinfachung. Die Größenordnung der Ungenauigkeit wird dabei durch die Rundungsstelle angegeben.

Wieso rundet man Zahlen?

Wieso runden wir überhaupt Zahlen 🤔? Naja, manchmal interessieren wir uns eben nicht so sehr für die Details, sondern ordnen Sachverhalte ein oder treffen Entscheidungen basierend auf einer anderen Größenordnung (Skala).

So ist vermutlich die exakte Anzahl der Zuschauer in einem Fußballstadion ⚽ (68.456 vs. 68.457 Zuschauer) für die Einsatzplanung der Polizei weniger relevant als die ungefähre Anzahl (60 vs. 70 Tausend Zuschauer).

Zudem ist es auf Grund von Messgenauigkeit manchmal auch gar nicht möglich eine bestimmte Größe exakt anzugeben. Für das Zuschauerbeispiel bedeutet dies, dass wir im Zweifel gar nicht wissen, ob es nun 68.456 oder 68.457 Zuschauer waren (Zuschauer sind nicht gekommen, haben das Stadion früher verlassen, …). Wenn also die Schätzung der Zuschauerzahl bereits eine gewisse Ungenauigkeit besitzt, macht eine exakte Angabe keinen Sinn. Die Ungenauigkeit gibt somit die Rundungsgenauigkeit vor.

Wie rundet man Zahlen? - Rundungsregeln 🚀

Wie du beim Runden einer natürliche Zahl vorgehen musst erklären wir dir anhand der folgenden zwei Beispiele:

Beispielaufgaben zum Runden auf verschieden Stellen

Schritt 1: Suche die relevanten Ziffern 👈

Anhand der Rundungsstelle (die in der Aufgabe angegeben sein sollte) findest du die beiden relevanten Ziffern für diese Aufgabe - die Rundungsstelle selbst sowie die Ziffer rechts neben der Rundungsstelle.

Wie rundet man Zahlen - Rundungsregeln Schritt 1

Die Rundungsstellen werden meist als “Runde auf Hunderter”, “Runde auf Tausender”, usw. angegeben. Falls du eine Auffrischung zu den Stellenwerten einer natürlichen Zahl benötigst, schau dir gerne unseren Artikel zur Stellenwerttafel an.

Schritt 2: Entscheide ob abgerundet wird 👈

Ist die Ziffer vor der Rundungsstelle kleiner als $5$ (also $0,1,2,3,4$ ), so wird abgerundet (wie in unserem ersten Beispiel)

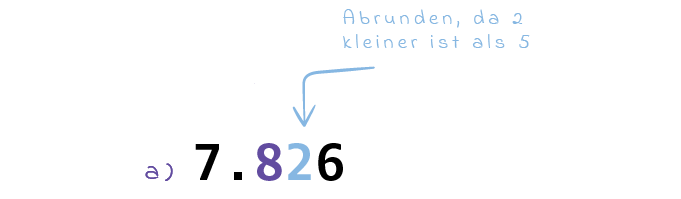
Wie rundet man Zahlen - Rundungsregeln Schritt 2

Wird nicht abgerundet kannst du übergehen zu Schritt 4 bzw. Schritt 5.

Schritt 3: Natürliche Zahl abrunden 👈

Beim Abrunden werden alle Ziffern rechts der Rundungsstelle gleich Null gesetzt (das ist beim Auf- und Abrunden gleich)

Die Rundungsstelle selbst bleibt unverändert

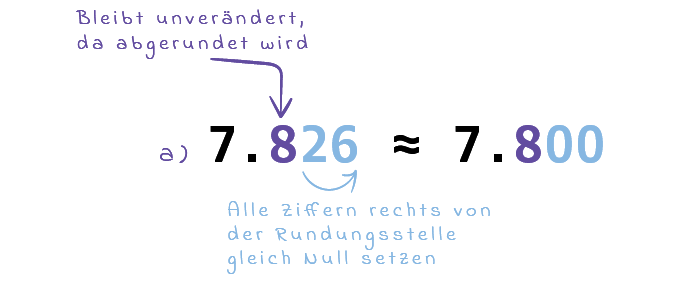
Wie rundet man Zahlen - Rundungsregeln Schritt 3

Schritt 4: Entscheide ob aufgerundet wird 👈

Ist die Ziffer vor der Rundungsstelle größer gleich $5$ (also $5,6,7,8,9$ ), so wird aufgerundet (wie in unserem zweiten Beispiel)

Wie rundet man Zahlen - Rundungsregeln Schritt 4

Schritt 5: Natürliche Zahl aufrunden 👈

Beim Abrunden werden alle Ziffern rechts der Rundungsstelle gleich Null gesetzt (das ist beim Auf- und Abrunden gleich)

Die Rundungsstelle selbst wird um 1 erhöht

Wie rundet man Zahlen - Rundungsregeln Schritt 5

Rundungszeichen

Um anzugeben, dass eine Zahl gerundet wurde, können wir das Rundungszeichen verwenden. Dieses gibt jedoch nicht mehr an, auf welche Stelle gerundet wurde.

Rundungszeichen	Beschreibung	Beispiel
$\sim$	…ungefähr…	$68.400 \sim 68.000 \\ (\text{68.400 ist ungefähr 68.000})$

Runden auf Zehner - Beispiele

In folgenden Beispielen runden wir natürliche Zahlen auf die Zehnerstelle

Natürliche Zahl	Auf Zehner gerundet	Auf-/Abrunden?
$56$	$\sim 60$	Aufrunden
$25.547$	$\sim 25.550$	Aufrunden
$344$	$\sim 340$	Abrunden
$4$	$\sim 0$	Abrunden

Runden auf Hunderter - Beispiele

In folgenden Beispielen runden wir natürliche Zahlen auf die Hunderterstelle

Natürliche Zahl	Auf Hunderter gerundet	Auf-/Abrunden?
$368$	$\sim 400$	Aufrunden
$18.556$	$\sim 18.600$	Aufrunden
$51$	$\sim 100$	Abrunden
$13.932$	$\sim 13.900$	Abrunden

Runden auf Tausender - Beispiele

In folgenden Beispielen runden wir natürliche Zahlen auf die Tausenderstelle

Natürliche Zahl	Auf Tausender gerundet	Auf-/Abrunden?
$5.963$	$\sim 6.000$	Aufrunden
$30.896$	$\sim 31.000$	Aufrunden
$12$	$\sim 0$	Abrunden
$6.285$	$\sim 6.000$	Abrunden

Runden einer natürlichen Zahl für verschiedene Rundungsstellen - Beispiele

In folgenden Beispielen runden wir die natürliche Zahl $1.395.064$ auf verschiedene Rundungsstellen

Rundungsstelle	Natürliche Zahl	Gerundet	Auf-/Abrunden?
Zehner	$1.395.064$	$\sim 1.395.060$	Abrunden
Hunderter	$1.395.064$	$\sim 1.395.100$	Aufrunden
Tausender	$1.395.064$	$\sim 1.395.000$	Abrunden
Zehntausender	$1.395.064$	$\sim 1.400.000$	Aufrunden
Hunderttausender	$1.395.064$	$\sim 1.400.000$	Aufrunden
Millionen	$1.395.064$	$\sim 1.000.000$	Abrunden

Fragen und Antworten

Ab welcher Zahl rundet man auf?

Ist die Ziffer rechst neben der Rundungsstelle größer gleich 5, also eine

5,6,7,8,9

wird aufgerundet.

Ab welcher Zahl rundet man ab?

Ist die Ziffer rechst neben der Rundungsstelle kleiner als 5, also eine

0,1,2,3,4

wird abgerundet.

Wieso rundet man Zahlen?

Durch das Runden können Aufgaben stark vereinfacht werden, allerdings wird damit auch ein Verlust der Genauigkeit in Kauf genommen.

Wie rundet man Zahlen?

Zahlen werden gerundet, indem alle Zahlen rechts neben der Rudungsstelle gleich Null gesetzt werden. Die Rundungsstelle selbst wird entweder um 1 erhöht (falls die Ziffer neben der Rundungsstelle eine

5,6,7,8,9

ist) oder bleibt unverändert (falls die Ziffer neben der Rundungsstelle eine

0,1,2,3,4

ist).

Mehr zu natürlichen Zahlen

Du suchst detailierte Informationen, wie zum Beispiel alle Teiler oder die Vielfachenmenge, zu einer bestimmten natürlichen Zahl? Dann wirst du hier fündig.

1-20

21-40

41-60

61-80

81-100

101-120

121-140

141-160

161-180

181-200

Zahlen Runden

Wieso rundet man Zahlen?

Wie rundet man Zahlen? - Rundungsregeln 🚀

Schritt 1: Suche die relevanten Ziffern 👈