Teilermengen

Stefan Vickers·09.05.2023

Die Menge aller Teiler einer natürlichen Zahl

a

nennt man die Teilermenge von

a

, oder kurz

T_a

Beispiel

Die natürliche Zahl $12$ lässt sich durch die Zahlen $1;2;3;4;6$ und $12$ ohne Rest teilen. Das bedeutet, $1;2;3;4;6$ und $12$ sind Teiler der $12$ und lassen sich in der Teilermenge $T_{12} = \{1;2;3;4;6;12\}$ zusammenfassen.

Teilermengen - Übersicht

Abgesehen von der $1$ besitzt jede natürliche Zahl $a$ eine Teilermenge $T_a$ mit mindestens zwei Elementen; der $1$ und der Zahl $a$ selbst. Die beiden Teiler $1$ und $a$ nennt man triviale Teiler. Besitzt eine Teilermenge nur diese zwei Elemente, so ist die natürliche Zahl $a$ eine Primzahl.

$13 \text{ ist eine Primzahl, da }T_{13} = \{1;13\}$

Bei allen anderen nicht-trivialen Teilern spricht man von echten Teilern.
Die Elemente der Teilermenge können zudem in komplementäre Teiler zusammengefasst werden. Dabei sind Teiler dann komplementär zueinander, wenn sich die natürliche Zahl $a$ aus dem Produkt der komplementären Teiler ergibt.

$\{1;12\}$ sind komplementäre Teiler, da $1\cdot 12 = 12$
$\{2;6\}$ sind komplementäre Teiler, da $2\cdot 6 = 12$
$\{3;4\}$ sind komplementäre Teiler, da $3\cdot 4 = 12$

Die Eigenschaft der komplementären Teiler ist insbesondere für die Bestimmung von Teilermengen hilfreich, wie wir später sehen werden.

Betrachtet man die Teilermengen $T_a$ , $T_b$ zweier natürlichen Zahlen, so ergeben sich interessante Eigenschaften für das Zahlenpaar $(a,b)$ . Haben die beiden Mengen, abgesehen von der $1$ , keinen gemeinsamen Teiler, so sind $a$ und $b$ teilerfremd zueinander, oder kurz $a \perp b$ . Existiert hingegen mindestens ein gemeinsamer Teiler verschieden von $1$ , so existiert auch ein groesster gemeinsamer Teiler, der für das Rechnen mit Brüchen relevant ist.

Alles was du zu Teilermengen wissen musst, haben wir in diesem Video für dich zusammengefasst. Schau gerne rein, wenn du eine Auffrischung brauchst.

Teilermengen bestimmen

Die Aufgabe, die Teilermenge $T_a$ einer natürlichen Zahl $a$ zu bestimmen, können wir anhand der Definition der Teilermenge abarbeiten, indem wir die Teilbarkeit für jede natürliche Zahl $n \leq a$ schrittweise prüfen.

Beispiel

Die Teilermenge der $12$ lässt sich wie folgt sukzessive bestimmen:

n	Teiler der 12?	Begründung
1	$12\mid 1$	1 ist trivialer Teiler
2	$12\mid 2$	Teilbarkeitsregel der 2
3	$12\mid 3$	Teilbarkeitsregel der 3
4	$12\mid 4$	Teilbarkeitsregel der 4
5	$12\nmid 5$	Teilbarkeitsregel der 5
6	$12\mid 6$	Teilbarkeitsregel der 6
7	$12\nmid 7$	$12:7 = 1 \text{ Rest } 5$
8	$12\nmid 8$	Teilbarkeitsregel der 8
9	$12\nmid 9$	Teilbarkeitsregel der 9
10	$12\nmid 10$	Teilbarkeitsregel der 10
11	$12\nmid 11$	$12:11 = 1 \text{ Rest } 1$
12	$12\mid 12$	12 ist trivialer Teiler

Aus der Tabelle lässt sich dann $T_{12} = \{1;2;3;4;6;12\}$ einfach ablesen.

Bei diesem Verfahren stellt man jedoch fest, dass es mit größer werdendem $a$ recht aufwändig ist, alle natürlichen Zahlen $n = \{0;1;2\dots;a\}$ auf Teilbarkeit zu prüfen. Um sich das Leben leichter zu machen, kann man sich der Eigenschaft der komplementären Teiler zu nutze machen. Wie dieser Trick funktioniert, zeigen wir dir im nächsten Abschnitt.

Du hättest lieber ein Video, das dir genau erklärt, wie man Teilermengen mit einem einfachen Trick bestimmt? Kein Problem:

Teilermengen bestimmen - Trick

Folgende zwei Eigenschaften von Teilern können wir ausnutzen, um diesen Trick zur Bestimmung einer Teilermenge $T_a$ anzuwenden

Haben wir eine natürliche Zahl $t_1$ gefunden, die Teiler von a ist, so ist auch $a:t_1= t_2$ ein Teiler von $a$ . Das bedeutet für unser Beispiel $T_{12}$ : Falls $2$ Teiler von $12$ ist, dann ist auch $12:2 = 6$ Teiler von $12$ .

Mit folgendem Beispiel können wir den Trick exemplarisch Schritt für Schritt demonstrieren

Kochrezept zur Bestimmung der Teilermengen | Trick - Aufgabenstellung

Schritt 1: Bestimme die obere Grenze 👈

Die obere Grenze $t_{max}$ , bis zu der wir alle natürlichen Zahlen auf Teilbarkeit prüfen müssen, erhalten wir aus der nach unten abgerundeten Wurzel der 44 $t_{max} = \lfloor \sqrt{44} \rfloor = 6$ .

Kochrezept zur Bestimmung der Teilermengen | Trick - Schritt 1: Die obere Grenze bestimmen

Schritt 2: Bestimme die obere Grenze (alternativer Weg) 👈

Falls dir die Wurzel einer Zahl noch nichts sagt, kein Problem. Du kannst die obere Grenze auch bestimmen indem du nach der größten natürlichen Zahl suchst, die mit sich selbst multipliziert gerade noch kleiner ist als $44$ ist.

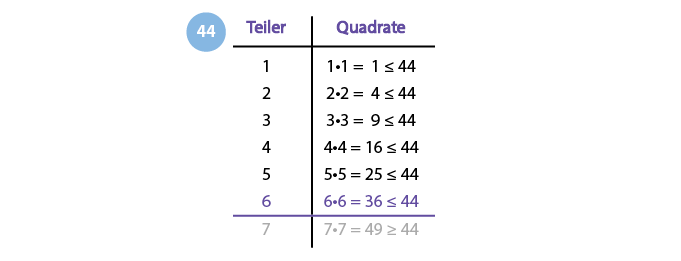
Kochrezept zur Bestimmung der Teilermengen | Trick - Aufgabenstellung - Schritt1: Die obere Grenze bestimmen (Alternativweg)

Schreibe dazu alle Teiler und die entsprechenden Quadratzahlen der Reihe nach beginnend bei der 1 in einer Tabelle. Sobald die erste Quadratzahl größer ist als $44$ hast du die obere Grenze gefunden.

Schritt 3: Schreibe alle Teiler auf 👈

Gehe nun alle Teiler bis zur oberen Grenze aus dem vorherigen Schritt durch und überprüfe auf Teilbarkeit (z.B. mit Hilfe der Teilbarkeitsregeln).

Kochrezept zur Bestimmung der Teilermengen | Trick - Aufgabenstellung - Schritt 3: Die Teiler aufschreiben

Schritt 4: Schreibe komplementäre Teiler auf 👈

Für alle gefunden Teiler kannst du nun in deiner Tabelle die komplementären Teiler dazu schreiben.

Kochrezept zur Bestimmung der Teilermengen | Trick - Aufgabenstellung - Schritt 4 - Die komplementären Teiler aufschreiben

Tipp: Schritt 3 und 4 kannst du auch gerne parallel durchführen.

Schritt 5: Teilermenge aufschreiben 👈

Notiere nun im letzten Schritt alle gefunden Teiler indem du dich U-förmig der Tabelle entlang vorarbeitest.

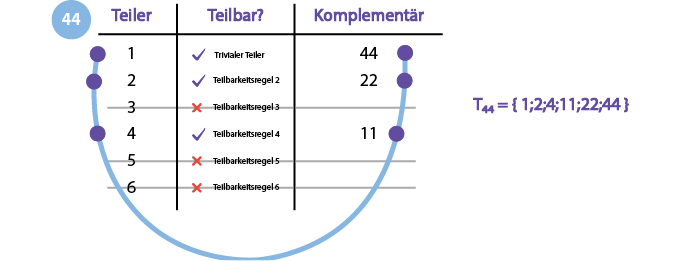
Kochrezept zur Bestimmung der Teilermengen | Trick - Aufgabenstellung - Schritt 5: Teiler im letzten Schritt aufschreiben

So erhältst du als Ergebnis die Teilermenge in aufsteigend geordneter Reihenfolge.

Wozu brauche ich das?

Teilermengen spielen insbesondere bei der Bruchrechnung sowie der Primfaktorzerlegung eine wichtige Rolle. Die Aufgaben aus den beiden Themengebiete lassen sich einfacher bewerkstelligen, wenn du dich bereits gut mit Teilermengen auskennst.

Beispiele für Teilermengen

Hier findest du Teilermengen einiger ausgewählter natürlicher Zahlen

Teilermenge	Link
$T_{30}$	Alle Teiler der 30
$T_{32}$	Alle Teiler der 32
$T_{42}$	Alle Teiler der 42
$T_{45}$	Alle Teiler der 45
$T_{48}$	Alle Teiler der 48
$T_{60}$	Alle Teiler der 60
$T_{72}$	Alle Teiler der 72
$T_{81}$	Alle Teiler der 81
$T_{90}$	Alle Teiler der 90

Teilermengen - Aufgaben mit Lösungen

Falls du gerne die Bestimmung von Teilermengen üben möchtest, dann hast du hier die Gelegenheit dir entweder bereits fertige Übungsblätter herunterzuladen, in unserem Aufgabengenerator eigene Übungsblätter zusammenzustellen oder direkt mit unserem Trainingscenter zu starten 🚀.

PDF zu einfachen Aufgaben und Lösungen zur Bestimmung von Teilermengen

PDF zu mittelschweren Aufgaben und Lösungen zur Bestimmung von Teilermengen

PDF zu schweren Aufgaben und Lösungen zur Bestimmung von Teilermengen

Aufgaben-Tool

Erstelle dir kostenlos Übungsblätter zu Teilermengen

Fragen und Antworten

Was ist eine Teilermenge?

Die Teilermenge fasst alle Teiler

n

einer natürlichen Zahl

a

in einer Menge

T_a

zusammen. Dabei sind die trivialen Teiler

1

und die Zahl

a

selbst stets Elemente der Teilermenge. Die Teilermenge der

14

enthält z.B. die Elemente

T_{14} = \{1;2;7;14\}

Mehr zu natürlichen Zahlen

Du suchst detailierte Informationen, wie zum Beispiel alle Teiler oder die Vielfachenmenge, zu einer bestimmten natürlichen Zahl? Dann wirst du hier fündig.

1-20

21-40

41-60

61-80

81-100

101-120

121-140

141-160

161-180

181-200

Teilermengen

Beispiel

Teilermengen - Übersicht

Teilermengen bestimmen

Beispiel

Teilermengen bestimmen - Trick

Schritt 1: Bestimme die obere Grenze 👈

Schritt 2: Bestimme die obere Grenze (alternativer Weg) 👈

Schritt 3: Schreibe alle Teiler auf 👈

Schritt 4: Schreibe komplementäre Teiler auf 👈

Schritt 5: Teilermenge aufschreiben 👈

Wozu brauche ich das?

Beispiele für Teilermengen

Teilermengen - Aufgaben mit Lösungen

Aufgaben-Tool

Fragen und Antworten

Mehr zu natürlichen Zahlen

Mathekönig

Individuelle Arbeitsblätter auf Knopfdruck

Lerninhalte

Infos

Rechtliches

Community

Teilermengen

Beispiel

Teilermengen - Übersicht

Teilermengen bestimmen

Beispiel

Teilermengen bestimmen - Trick

Schritt 1: Bestimme die obere Grenze 👈

Schritt 2: Bestimme die obere Grenze (alternativer Weg) 👈

Schritt 3: Schreibe alle Teiler auf 👈

Schritt 4: Schreibe komplementäre Teiler auf 👈

Schritt 5: Teilermenge aufschreiben 👈

Wozu brauche ich das?

Beispiele für Teilermengen

Teilermengen - Aufgaben mit Lösungen

Aufgaben-Tool

Fragen und Antworten

Das könnte dich auch interessieren

Mehr zu natürlichen Zahlen

Mathekönig

Individuelle Arbeitsblätter auf Knopfdruck

Lerninhalte

Infos

Rechtliches

Community