Schriftlich Multiplizieren einfach erklärt
Verstehe wie die schriftliche Multiplikation funktioniert und stelle dir individuelle Übungsblätter samt Lösungen zum Thema zusammen.
30.11.2023·Grundrechenarten erklärt
MathekönigBrüche - Einführung
Stefan Vickers·09.05.2023
Brüche oder Bruchzahlen beschreiben einen Anteil in Bezug auf eine bestimmte Größe. Dabei kann diese Bezugsgröße z.B. ein Gegenstand (ein Kuchen, eine Grundstücksfläche, 50 Murmeln, ….), eine Personengruppe (die Klasse 5d, alle Menschen über 50 Jahre, … ), eine Maßeinheit (5km Schulweg, 200g Butter, 8 Liter Wasser, …) oder irgendetwas anderes darstellen, das sich in einer sinnvollen Art und Weise aufteilen lässt.
So kann z.B. eine Pizza in 8 gleich große Anteile (bei Pizza würde man vermutlich eher von Stücken sprechen 😉) aufgeteilt und anschließend verteilt werden. Wenn Hendrik nun 2 dieser 8 gleichgroßen Stücke isst, hat er insgesamt zwei Achtel, bzw.
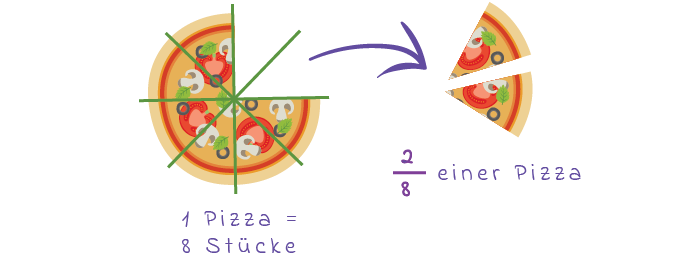
Im Alltag ist uns der Gebrauch von Brüchen durchaus nicht fremd, jedoch geschieht dies meist ohne konkret an Brüche zu denken. So spielen z.B. Musiker Halbe, Viertel oder Achtel Noten, wir kaufen im Supermarkt einen halben Liter Milch ein und treffen uns mit unseren Freunden eine Viertelstunde nach drei.
Diese im Alltag gängige Verwendung von Brüchen lässt sich durch die Mathematik verallgemeinern und erlaubt uns somit Brüche über den einfachen sprachlichen Gebrauch hinaus zu verwenden, wodurch wir z.B. Brüche formal vergleichen, addieren und subtrahieren oder multiplizieren und dividieren können.
Achtung! Ein Bruch bzw. Anteil bezieht sich stets auf eine bestimmte Bezugsgröße. In manchen Fällen kann es vorkommen, dass diese Bezugsgröße nicht explizit angegeben wird und sich nur aus dem Kontext erschließen lässt. So bezieht sich z.B. die Zeitangabe viertel nach drei auf ein viertel einer ganzen Stunde
Brüche - Die Grundlagen
Brüche werden durch zwei natürliche Zahlen dargestellt, die durch einen Bruchstrich getrennt werden. Dabei wird die Zahl oberhalb des Bruchstrichs als Zähler und die Zahl unterhalb des Bruchstrichs als Nenner bezeichnet.
Der Nenner bestimmt die Anzahl aller Anteile, in der etwas zerteilt wurde (in unserem Beispiel waren es 8 Pizzastücke). Der Zähler gibt an, wie viele Anteile jemand z.B. besitzt oder gegessen hat (in unserem Beispiel 2 Stücke Pizza).
Wie bereits erwähnt, bezieht sich ein Bruch stets auf eine bestimmte Bezugsgröße. Diese Bezugsgröße bezeichnet man auch als “Ganzes”. Die Bruchzahl ist dann in diesem Zusammenhang der Anteil vom Ganzen und die tatsächlichen Anteile an dem “Ganzen” wiederum nennt man Bruchteil.
Wie man aus dem Zusammenhang zwischen dem Ganzen, dem Anteil sowie dem Bruchteil erkennen kann, lässt sich eine Bruchzahl auch als eine Division mit dem Nenner sowie eine Multiplikation mit dem Zähler verstehen.
So werden in dem obigen Beispiel 180km (das “Ganze”) in insgesamt 6 gleich große Teilstrecken (
Das könnte dich auch interessieren
